题目内容
如图,以ox为始边作角α与β(0<β<α<π),它们的终边分别与单位圆相交于点P、Q,已知点的坐标为 .
.
(Ⅰ)求 的值;
的值;
(Ⅱ)若 ,求sin(α+β).
,求sin(α+β).
解:(Ⅰ)由任意角的三角函数的定义可得 sinα= ,cosα=-
,cosα=- ,tanα=-
,tanα=- .
.
∴sin2α=2sinαcosα=- ,cos2α=cos2α-sinα2=-
,cos2α=cos2α-sinα2=- .
.
∴ =
= =
=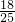 .
.
(Ⅱ)若 ,则 β-α=
,则 β-α= ,β+α=2α-
,β+α=2α- ,
,
∴sin(α+β)=sin(2α- )=-cos2α=
)=-cos2α= .
.
分析:题干错误,应该:点P 的坐标为 .
.
(Ⅰ)由任意角的三角函数的定义求出 sinα、cosα、tanα 的值,再利用二倍角的正弦、余弦公式求得sin2α、cos2α 的值,代入要求的式子花简求得结果.
(Ⅱ)若 ,则有 β+α=2α-
,则有 β+α=2α- ,再由sin(α+β)=sin(2α-
,再由sin(α+β)=sin(2α- )=-cos2α,运算求得结果.
)=-cos2α,运算求得结果.
点评:本题主要考查任意角的三角函数的定义,二倍角的正弦、余弦公式的应用,属于中档题.
 ,cosα=-
,cosα=- ,tanα=-
,tanα=- .
. ∴sin2α=2sinαcosα=-
 ,cos2α=cos2α-sinα2=-
,cos2α=cos2α-sinα2=- .
.∴
 =
= =
=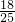 .
.(Ⅱ)若
 ,则 β-α=
,则 β-α= ,β+α=2α-
,β+α=2α- ,
,∴sin(α+β)=sin(2α-
 )=-cos2α=
)=-cos2α= .
.分析:题干错误,应该:点P 的坐标为
 .
.(Ⅰ)由任意角的三角函数的定义求出 sinα、cosα、tanα 的值,再利用二倍角的正弦、余弦公式求得sin2α、cos2α 的值,代入要求的式子花简求得结果.
(Ⅱ)若
 ,则有 β+α=2α-
,则有 β+α=2α- ,再由sin(α+β)=sin(2α-
,再由sin(α+β)=sin(2α- )=-cos2α,运算求得结果.
)=-cos2α,运算求得结果.点评:本题主要考查任意角的三角函数的定义,二倍角的正弦、余弦公式的应用,属于中档题.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
如图,以Ox为始边作任意角α,β,它们的终边与单位圆分别交于A,B点,则
•
的值等于( )
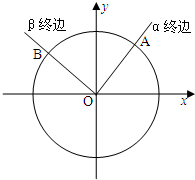
| OA |
| OB |

| A、sin(α+β) |
| B、sin(α-β) |
| C、cos(α+β) |
| D、cos(α-β) |
 如图,以Ox为始边作角α与β(0<β<α<π),它们的终边分别与单位圆相交于点P,Q,已知点P的坐标为
如图,以Ox为始边作角α与β(0<β<α<π),它们的终边分别与单位圆相交于点P,Q,已知点P的坐标为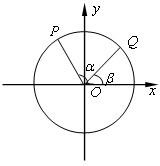
 .
. 的值;
的值; ,求sin(α+β).
,求sin(α+β).