Question

【题目】函数是定义在上的奇函数，且为偶函数，当时，，若函数恰有一个零点，则实数的取值范围是

A. B.

C. D.

Answer 1

【答案】D

【解析】分析：根据条件判断函数的周期性和对称性，求出函数在一个周期内的解析式，利用转化法进行求解即可．

详解：∵f（x）是定义在R上的奇函数，且f（x﹣1）为偶函数，

∴f（﹣x﹣1）=f（x﹣1）=﹣f（x+1），

即f（x）=﹣f（x+2），

则f（x+4）=﹣f（x+2）=f（x），即函数f（x）的周期是4，

∵f（x﹣1）为偶函数，∴f（x﹣1）关于x=0对称，

则f（x）关于x=﹣1对称，同时也关于x=1对称，

若x∈[﹣1，0]，则﹣x∈[0，1]，

此时f（﹣x）==﹣f（x），则f（x）=﹣，x∈[﹣1，0]，

若x∈[﹣2，﹣1]，x+2∈[0，1]，

则f（x）=﹣f（x+2）=﹣，x∈[﹣2，﹣1]，

若x∈[1，2]，x﹣2∈[﹣1，0]，

则f（x）=﹣f（x﹣2）==，x∈[1，2]，

作出函数f（x）的图象如图：

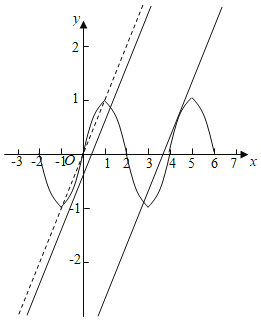
由数g（x）=f（x）﹣x﹣b=0得f（x）=x+b，

由图象知当x∈[﹣1，0]时，由﹣=x+b，平方得x2+（2b+1）x+b2=0，

由判别式△=（2b+1）2﹣4b2=0得4b+1=0，得b=﹣，此时f（x）=x+b有两个交点，

当x∈[4，5]，x﹣4∈[0，1]，则f（x）=f（x﹣4）=，

由=x+b，平方得x2+（2b﹣1）x+4+b2=0，

由判别式△=（2b﹣1）2﹣16﹣4b2=0得4b=﹣15，得b=﹣，此时f（x）=x+b有两个交点，

则要使此时f（x）=x+b有一个交点，则在[0，4]内，b满足﹣＜b＜﹣，

即实数b的取值集合是4n﹣＜b＜4n﹣，

即4（n﹣1）+＜b＜4（n﹣1）+，

令k=n﹣1，

则4k+＜b＜4k+，

故选：D．