题目内容
如果满足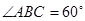 ,
,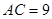 ,
,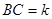 的△ABC恰有一个,那么
的△ABC恰有一个,那么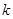 的取值范围是 ;
的取值范围是 ;
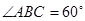 ,
,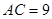 ,
,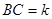 的△ABC恰有一个,那么
的△ABC恰有一个,那么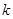 的取值范围是 ;
的取值范围是 ;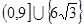
试题分析:要对三角形解得各种情况进行讨论即:无解、有1个解、有2个解,从中得出恰有一个解时k满足的条件.根据题意,由于满足
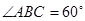 ,
,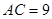 ,
,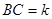 的△ABC恰有一个,则可知解:(1)当AC<BCsin∠ABC,即9<ksin60°,即k>6
的△ABC恰有一个,则可知解:(1)当AC<BCsin∠ABC,即9<ksin60°,即k>6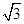 时,三角形无解;(2)当AC=BCsin∠ABC,即12=ksin60°,即k=6
时,三角形无解;(2)当AC=BCsin∠ABC,即12=ksin60°,即k=6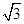 时,三角形有1解;(3)当AC<BCsin∠ABC<BC,即ksin60°<9<k,即9<k<6
时,三角形有1解;(3)当AC<BCsin∠ABC<BC,即ksin60°<9<k,即9<k<6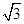 ,三角形有2个解;(4)当0<BC≤AC,即0<k≤9时,三角形有1个解.综上所述:当0<k≤9或k=6
,三角形有2个解;(4)当0<BC≤AC,即0<k≤9时,三角形有1个解.综上所述:当0<k≤9或k=6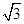 时,三角形恰有一个解.故答案为
时,三角形恰有一个解.故答案为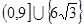
点评:本题属于解三角形的题型,主要考查了三角形解个数的问题,重在分情况分类讨论.易错点在于可能漏掉 k情况.

练习册系列答案
相关题目
 中
中 ,
, ,则
,则 =( )
=( )



 中,
中, 为
为 边上的点
边上的点 ,且
,且 .
.
 ;
; ,求
,求 .
. 中,已知
中,已知 求∠A,∠C,边c.
求∠A,∠C,边c. ,且
,且
 的大小;(2)若
的大小;(2)若 且
且 求
求
 的角A、B、C所对的边分别是
的角A、B、C所对的边分别是 ,
, ,
,  ,
, 
 ∥
∥ ,求证:
,求证: ,边长
,边长 ,
, ,求
,求 ,A=30°,则c的值为( )。
,A=30°,则c的值为( )。
 ,函数
,函数
 的最小正周期;
的最小正周期; 分别为△ABC内角A,B,C的对边,
分别为△ABC内角A,B,C的对边, ,且
,且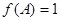 ,求A和△ABC面积的最大值。
,求A和△ABC面积的最大值。 中,
中, 为角
为角 所对的边,且
所对的边,且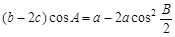 。
。 的值; (2)若
的值; (2)若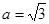 ,则求
,则求 的取值范围。
的取值范围。