题目内容
设椭圆
+
=1的焦点在y轴上,a∈{1,2,3,4,5},b∈{1,2,3,4,5,6},则这样的椭圆个数为( )
| x2 |
| a2 |
| y2 |
| b2 |
| A、10 | B、15 | C、20 | D、25 |
考点:椭圆的标准方程
专题:计算题,概率与统计
分析:根据题意,由椭圆的焦点在y轴上,分析可得b2>a2,结合a∈{1,2,3,4,5},b∈{1,2,3,4,5,6},对a、b进行分类讨论,由分类加法原理计算可得答案.
解答:
解:椭圆
+
=1的焦点在y轴上,必有b2>a2,
而a∈{1,2,3,4,5},b∈{1,2,3,4,5,6},
当a=1时,b可取的值为2、3、4、5、6,共5种情况;
当a=2时,b可取的值为3、4、5、6,共4种情况;
当a=3时,b可取的值为4、5、6,共3种情况;
当a=4时,b可取的值为5、6,共2种情况;
当a=5时,b可取的值为6,只有1种情况;
则共有5+4+3+2+1=15种情况,即有15个这样的椭圆;
故选:B.
| x2 |
| a2 |
| y2 |
| b2 |
而a∈{1,2,3,4,5},b∈{1,2,3,4,5,6},
当a=1时,b可取的值为2、3、4、5、6,共5种情况;
当a=2时,b可取的值为3、4、5、6,共4种情况;
当a=3时,b可取的值为4、5、6,共3种情况;
当a=4时,b可取的值为5、6,共2种情况;
当a=5时,b可取的值为6,只有1种情况;
则共有5+4+3+2+1=15种情况,即有15个这样的椭圆;
故选:B.
点评:本题考查椭圆的标准方程,涉及分类计数原理的应用,要牢记椭圆的标准方程形式以及焦点位置的判断方法.

练习册系列答案
 激活思维优加课堂系列答案
激活思维优加课堂系列答案 活力试卷系列答案
活力试卷系列答案
相关题目
设全集U=R,A={x|x(x+2)<0,B={x|x<-1},则图中阴影部分表示的集合为( )
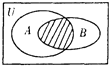

| A、{x|-2<x<0} |
| B、{x|-2<x<-1} |
| C、{x|x>0} |
| D、{x|x<-1} |
若α,β是两个不同平面,m,n是两条不同直线,则下列命题中不正确的是( )
| A、α∥β,m⊥α,则m⊥β |
| B、m∥n,m⊥α,则n⊥α |
| C、n∥α,n⊥β,则α⊥β |
| D、α∩β=m,n与α,β所成的角相等,则m⊥n |
cos(α-35°)cos(α+25°)+sin(α-35°)sin(α+25°)等于( )
A、
| ||||
B、-
| ||||
C、
| ||||
D、-
|
如图,网格纸上的正方形的边长为1,粗线画出的是某几何体的三视图,则这个几何体的体积为( )


| A、30 | B、50 | C、75 | D、150 |
非零向量
,
满足|
|=|
|=|
+
|,则
与
的夹角为( )
| a |
| b |
| a |
| b |
| a |
| b |
| a |
| b |
A、
| ||
B、
| ||
C、
| ||
D、
|
执行下面的框图,若输入的n是6,则输出p的值是( )


| A、120 | B、720 |
| C、1440 | D、5040 |
已知数列1,
,
,2,
,…则3
是它的( )
| 2 |
| 3 |
| 5 |
| 3 |
| A、第25项 | B、第26项 |
| C、第27项 | D、第28项 |