题目内容
（2013•丽水一模）在△ABC中，角A，B，C所对的边分别为a，b，c，若3bcosA=ccosA+acosC，则tanA的值是（ ）
分析：根据余弦定理，化简可得ccosA+acosC=b，从而将等式3bcosA=ccosA+acosC化简得到cosA=
＞0，由同角三角函数的平方关系算出sinA=
，再由商数关系即可得到tanA的值．
| 1 |
| 3 |
2
| ||
| 3 |
解答：解：∵△ABC中，由余弦定理得
ccosA+acosC=c×
+a×
=b
∴根据题意，3bcosA=ccosA+acosC=b
两边约去b，得3cosA=1，所以cosA=
＞0
∴A为锐角，且sinA=
=
因此，tanA=
=2
故选：C
ccosA+acosC=c×
| b2+c2-a2 |
| 2bc |
| a2+b2-c2 |
| 2ab |
∴根据题意，3bcosA=ccosA+acosC=b
两边约去b，得3cosA=1，所以cosA=
| 1 |
| 3 |
∴A为锐角，且sinA=
| 1-cos2A |
2
| ||
| 3 |
因此，tanA=
| sinA |
| cosA |
| 2 |
故选：C
点评：本题给出三角形中的边角关系式，求tanA的值．着重考查了余弦定理解三角形、同角三角函数的基本有关系等知识，属于基础题．
练习册系列答案
相关题目
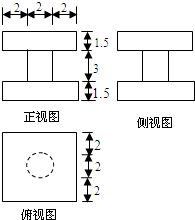（2013•丽水一模）某几何体的三视图如图所示，则该几何体的体积为
（2013•丽水一模）已知抛物线的顶点在坐标原点，焦点在y轴上，且过点（2，1），