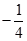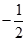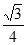题目内容
已知函数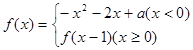 ,且函数
,且函数 恰有3个不同的零点,则实数
恰有3个不同的零点,则实数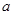 的取值范围是
的取值范围是
A. | B. | C.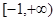 | D.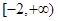 |
C
解析试题分析:因为当x≥0的时候,f(x)=f(x-1),所以所有大于等于0的x代入得到的
f(x)相当于在[-1,0)重复的周期函数,
x∈[-1,0)时, ,对称轴x=-1,顶点(-1,1+a)
,对称轴x=-1,顶点(-1,1+a)
(1)如果a<-1,函数y=f(x)-x至多有2个不同的零点;
(2)如果a=-1,则y有一个零点在区间(-1,0),有一个零点在(-∞,-1),一个零点是原点;
(3)如果a>-1,则有一个零点在(-∞,-1),y右边有两个零点,
故实数a的取值范围是[-1,+∞)
故选C.
考点:本题主要考查分段函数的概念,函数零点的概念,函数图象和性质。
点评:典型题,本题通过分析函数的特征,明确其为周期函数,从而对函数图象有了全面认识,确定了函数零点所在区间。分类讨论思想的应用是关键。

练习册系列答案
 期末冲刺100分创新金卷完全试卷系列答案
期末冲刺100分创新金卷完全试卷系列答案
相关题目
下列函数中,既是奇函数又是区间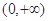 上的增函数的是( )
上的增函数的是( )
A.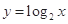 | B.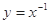 | C.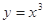 | D.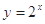 |
若定义在R上的偶函数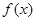 满足
满足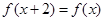 ,且当
,且当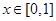 时,
时,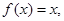 则方程
则方程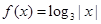 的解个数是 ( )
的解个数是 ( )
| A.0个 | B.2个 | C.4个 | D.6个 |
设f(x)是定义在R上的奇函数,当x≤0时,f(x)=2x2-x,则f(1)=
| A.-3 | B.-1 | C.1 | D.3 |
已知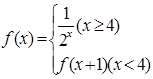 ,则
,则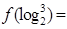 ( )
( )
A.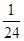 | B.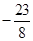 | C.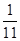 | D.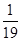 |
已知函数 满足
满足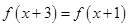 ,且
,且 ∈[-1,1]时,
∈[-1,1]时,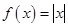 ,则函数
,则函数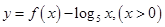 的零点个数是( )
的零点个数是( )
| A.3 | B.4 | C.5 | D.6 |
设函数 为定义在R上的奇函数,当
为定义在R上的奇函数,当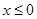 时,
时, (
( 为常数),则
为常数),则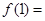 ( )
( )
| A.3 | B.1 | C.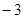 | D. |
下列各组函数中表示同一函数的是( )
A.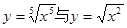 | B.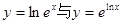 |
C. | D.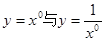 |
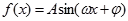 (
(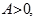
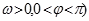 的部分图像如图所示.若△EFG为等腰直角三角形,且
的部分图像如图所示.若△EFG为等腰直角三角形,且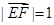 ,则
,则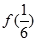 的值为 ( )
的值为 ( )