题目内容
17.已知函数f(x)=|x-2a|+|x-a|,x∈R,a≠0(1)当a=1时,解不等式:f(x)>2
(2)若b∈R,证明:f(b)≥f(a),并求在等号成立时$\frac{b}{a}$的范围.
分析 (1)由条件利用绝对值的意义求得不等式的解集.
(2)由条件利用绝对值三角不等式证得f(b)≥f(a),当且仅当b-2a与b-a同号,或它们中至少有一个为0时,取等号,再由(2a-b)(b-a)≥0,即 ${(\frac{b}{a})}^{2}$-3$\frac{b}{a}$+2≤0,求得$\frac{b}{a}$的范围.
解答 解:(1)当a=1时,解不等式:f(x)>2,即|x-2|+|x-1|>2,
|x-2|+|x-1|表示数轴上的x对应点到2、1对应点的距离之和,
而0.5和2.5对应点到2、1对应点的距离之和正好等于2,故不等式的解集为{x|x<0.5,或 x>2.5}.
(2)证明:∵f(x)=|x-2a|+|x-a|,
故 f(a)=f(a),f(b)=|b-2a|+|b-a|=|2a-b|+|b-a|≥|2a-b+b-a|=|a|,
即 f(b)≥f(a),当且仅当b-2a与b-a同号,或它们中至少有一个为0时,取等号,
∴(2a-b)(b-a)≥0,即 3ab-2a2-b2≥0,即 ${(\frac{b}{a})}^{2}$-3×$\frac{b}{a}$+2≤0,
求得1≤$\frac{b}{a}$≤2.
点评 本题主要考查绝对值的意义,绝对值三角不等式,一元二次不等式的解法,属于中档题.

练习册系列答案
相关题目
7.某几何体的三视图如图所示,则这个几何体外接球的表面积为( )
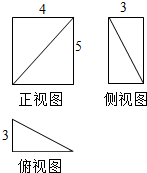

| A. | 20π | B. | 40π | C. | 50π | D. | 60π |
12.设集合A,B分别是函数y=log3(9-x2)的定义域和值域,则A∩B=( )
| A. | (-3,2) | B. | (-3,2] | C. | (0,2] | D. | (0,2) |
2.已知i为虚数单位,则|$\frac{2+4i}{1+\sqrt{3}i}$|=( )
| A. | $\frac{\sqrt{5}}{2}$ | B. | $\sqrt{5}$ | C. | 2$\sqrt{5}$ | D. | 5 |
9.已知单位向量$\overrightarrow{a}$,$\overrightarrow{b}$,满足$\overrightarrow{a}$•$\overrightarrow{b}$=0,且|$\overrightarrow{c}$-$\overrightarrow{a}$|+|$\overrightarrow{c}$-2$\overrightarrow{b}$|=$\sqrt{5}$,则|$\overrightarrow{c}$+2$\overrightarrow{a}$|的取值范围是( )
| A. | [1,3] | B. | [2$\sqrt{2}$,3] | C. | [$\frac{6\sqrt{5}}{5}$,2$\sqrt{2}$] | D. | [$\frac{6\sqrt{5}}{5}$,3] |
6.已知$a={(\frac{1}{2})^3},b={3^{\frac{1}{2}}},c={log_{\frac{1}{2}}}3$,则a,b,c之间的大小关系为( )
| A. | a>b>c | B. | b>a>c | C. | b>c>a | D. | a>c>b |
 如图,椭圆C1:$\frac{x^2}{a^2}+\frac{y^2}{b^2}$=1(a>0,b>0)和圆C2:x2+y2=b2,已知圆C2将椭圆C1的长轴三等分,且圆C2的面积为π,椭圆C1的下顶点为E,过坐标原点O且与坐标轴不重合的任意直线l与圆C2相交于点A、B,直线EA、EB与椭圆C1的另一个交点分别是点P、M.
如图,椭圆C1:$\frac{x^2}{a^2}+\frac{y^2}{b^2}$=1(a>0,b>0)和圆C2:x2+y2=b2,已知圆C2将椭圆C1的长轴三等分,且圆C2的面积为π,椭圆C1的下顶点为E,过坐标原点O且与坐标轴不重合的任意直线l与圆C2相交于点A、B,直线EA、EB与椭圆C1的另一个交点分别是点P、M.