题目内容
在直角坐标系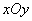 中,曲线
中,曲线 的参数方程为
的参数方程为 (
( 为参数),若以该直角坐标系的原点
为参数),若以该直角坐标系的原点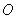 为极点,
为极点,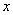 轴的正半轴为极轴建立极坐标系,曲线
轴的正半轴为极轴建立极坐标系,曲线 的极坐标方程为:
的极坐标方程为: (其中
(其中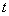 为常数).
为常数).
(1)若曲线 与曲线
与曲线 只有一个公共点,求
只有一个公共点,求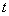 的取值范围;
的取值范围;
(2)当 时,求曲线
时,求曲线 上的点与曲线
上的点与曲线 上点的最小距离.
上点的最小距离.
(1) 或
或 ;(2)
;(2) .
.
【命题立意】本题旨在考查参数方程与普通直角坐标方程的转化与应用,函数与方程思维,点到直线的距离公式.
【解析】对于曲线M,消去参数,得普通方程为 ,曲线
,曲线 是抛物线的一部分; 对于曲线N,化成直角坐标方程为
是抛物线的一部分; 对于曲线N,化成直角坐标方程为 ,曲线N是一条直线. (2分)
,曲线N是一条直线. (2分)
(1)若曲线M,N只有一个公共点,则有直线N过点 时满足要求,并且向左下方平行运动直到过点
时满足要求,并且向左下方平行运动直到过点 之前总是保持只有一个公共点,再接着向左下方平行运动直到相切之前总是有两个公共点,所以
之前总是保持只有一个公共点,再接着向左下方平行运动直到相切之前总是有两个公共点,所以 满足要求;相切时仍然只有一个公共点,由
满足要求;相切时仍然只有一个公共点,由 ,得
,得
 ,求得
,求得 . 综合可求得
. 综合可求得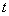 的取值范围是:
的取值范围是: 或
或 . (6分)
. (6分)
(2)当 时,直线N:
时,直线N:  ,设M上点为
,设M上点为 ,
, ,则
,则
 ,
,
当 时取等号,满足
时取等号,满足 ,所以所求的最小距离为
,所以所求的最小距离为 . (10分)
. (10分)

练习册系列答案
相关题目
 ,
, 满足约束条件
满足约束条件 则
则 的最小值
的最小值 为
为 B. 6 C.
B. 6 C.  D. 4
D. 4 B.
B. C.
C. D.
D. 
 ,设成绩在[80,90)这一小组中被抽中的学生中能通过复试的人数为
,设成绩在[80,90)这一小组中被抽中的学生中能通过复试的人数为 ,求
,求
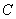 的极坐标方程为
的极坐标方程为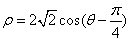 ,以极点
,以极点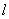 的参数方程为
的参数方程为 (
( ,则线段
,则线段 的长度是( )
的长度是( ) C.7 D.5
C.7 D.5 (
( 为参数,r为常数,r>0).以原点O为极点,x轴的正半轴为极轴建立极坐标系,直线l的极坐标方程为
为参数,r为常数,r>0).以原点O为极点,x轴的正半轴为极轴建立极坐标系,直线l的极坐标方程为 .若直线l与曲线C交于A,B两点,且
.若直线l与曲线C交于A,B两点,且 ,求r的值.
,求r的值. 中,已知
中,已知 是
是 的平分线,
的平分线, 的外接圆交
的外接圆交 于点
于点 .若
.若 ,
, ,求
,求 的长.
的长.