Question

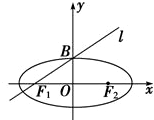
直线l：x-2y+2=0过椭圆的左焦点F₁和一个顶点B，则椭圆的方程为 ________．

Answer 1

分析：先设左焦点坐标为：（-c，0），顶点（0，b），由这两个点都在直线l：x-2y+2=0上，可解得b，c，进而解得a，从而求得椭圆方程．
解答：设左焦点坐标为：（-c，0），顶点（0，b）
根据题意：
∴
∴a=
∴椭圆的方程为
故答案为：
点评：本题主要考查点与直线的位置关系以及椭圆方程的求法．