题目内容
直线l:x+2y-2=0交y轴于点B,光线自点A(-1,4)射到点B后经直线l反射,求反射光线所在直线的方程.分析:先求出点A(-1,4)关于直线l的对称点A'的坐标,则A'在反射线上,又反射线经过点B(0,1),由截距式写出反射线的方程,并化为一般式.
解答:解:如图,设点A(-1,4)关于直线l的对称点A'(x0,y0)则
∴
,
∴
,∴A'(-3,0).
由反射定律知,A'在反射线上,又反射线经过点B(0,1),由截距式写出反射线的方程
+
=1,
即x-3y+3=0,所以,反射光线所在直线方程为x-3y+3=0.
∴
|
∴
|
由反射定律知,A'在反射线上,又反射线经过点B(0,1),由截距式写出反射线的方程
| x |
| -3 |
| y |
| 1 |
即x-3y+3=0,所以,反射光线所在直线方程为x-3y+3=0.
点评:本题考查求一个点关于直线的对称点的坐标的方法,直线的截距式方程.

练习册系列答案
相关题目
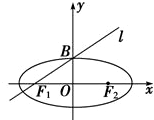
直线l:x-2y+2=0过椭圆左焦点F1和一个顶点B,则该椭圆的离心率为( )

A、
| ||||
B、
| ||||
C、
| ||||
D、
|
直线l:x-2y+2=0过双曲线的左焦点F1和一个虚顶点B,该双曲线的离心率为( )
A、
| ||||
B、
| ||||
C、
| ||||
| D、2 |