题目内容
6.设P为椭圆$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0)上任一点,F1,F2为椭圆的左右焦点,短轴的两个顶点与右焦点的连线构成等边三角形.(I)求椭圆的离心率;
(Ⅱ)直线l:y=kx+$\frac{b}{2}$与圆:x2+y2=$\frac{{b}^{2}}{5}$相切,且与椭圆交于P、Q两点,当△OPQ的面积等于$\sqrt{7}$,求椭圆的标准方程.
分析 (I)根据等边三角形可得a=2b,再利用a,b,c的关系得出a与c的关系,从而得出离心率;
(II)利用直线与圆相切列方程计算k,得出直线L的方程,与椭圆方程联立方程组消元,利用根与系数的关系计算|PQ|,得出三角形OPQ的面积,根据面积解出a,b即可.
解答 解:(I)∵短轴的两个顶点与右焦点的连线构成等边三角形,
∴a=2b,即b=$\frac{a}{2}$,∴c=$\sqrt{{a}^{2}-{b}^{2}}$=$\frac{\sqrt{3}}{2}$a,
∴e=$\frac{c}{a}$=$\frac{\sqrt{3}}{2}$.
(II)∵直线L:y=kx+$\frac{b}{2}$与圆:x2+y2=$\frac{{b}^{2}}{5}$相切,
∴$\frac{\frac{b}{2}}{\sqrt{{k}^{2}+1}}$=$\frac{b}{\sqrt{5}}$,解得k=$±\frac{1}{2}$.
设P(x1,y1),Q(x2,y2),
(1)若k=$\frac{1}{2}$,联立方程组$\left\{\begin{array}{l}{y=\frac{1}{2}x+\frac{b}{2}}\\{\frac{{x}^{2}}{{a}^{2}}+\frac{{y}^{2}}{{b}^{2}}=1}\\{a=2b}\end{array}\right.$,消元得:2x2+2bx-3b2=0,
△=4b2+24b2=28b2>0,
∴x1+x2=-b,x1x2=-$\frac{3}{2}{b}^{2}$,
∴|PQ|=(1+$\frac{1}{4}$)$\sqrt{({x}_{1}+{x}_{2})^{2}-4{x}_{1}{x}_{2}}$=$\frac{5\sqrt{7}}{4}b$,
∴S△OPQ=$\frac{1}{2}×\frac{5\sqrt{7}}{4}b×\frac{b}{\sqrt{5}}$=$\sqrt{7}$,解得b2=$\frac{8\sqrt{5}}{5}$,
∴a2=4b2=$\frac{32\sqrt{5}}{5}$,
∴椭圆方程为$\frac{{x}^{2}}{\frac{32\sqrt{5}}{5}}+\frac{{y}^{2}}{\frac{8\sqrt{5}}{5}}=1$.
(2)若k=-$\frac{1}{2}$,联立方程组$\left\{\begin{array}{l}{y=-\frac{1}{2}x+\frac{b}{2}}\\{\frac{{x}^{2}}{{a}^{2}}+\frac{{y}^{2}}{{b}^{2}}=1}\\{a=2b}\end{array}\right.$,消元得:2x2-2bx-3b2=0,
△=4b2+24b2=28b2>0,
∴x1+x2=b,x1x2=-$\frac{3}{2}{b}^{2}$,
以下解法同(1),
综上,椭圆的标准方程为$\frac{{x}^{2}}{\frac{32\sqrt{5}}{5}}+\frac{{y}^{2}}{\frac{8\sqrt{5}}{5}}=1$.
点评 本题考查了椭圆的性质,直线与圆、椭圆的位置关系,属于中档题.

| A. | (-2,-1) | B. | (1,2) | C. | (-3,-2) | D. | (2,3) |
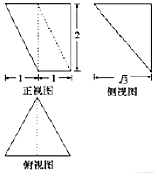
| A. | $\frac{11}{6}$$\sqrt{3}$ | B. | $\sqrt{3}$ | C. | $\frac{5\sqrt{3}}{3}$ | D. | $\frac{4\sqrt{3}}{3}$ |
| A. | [0,9] | B. | [5,+∞) | C. | $[\frac{{3\sqrt{2}}}{2},+∞)$ | D. | $[\frac{9}{2},+∞)$ |
| A. | 3 | B. | e+1 | C. | e | D. | e-1 |
| A. | $\frac{{3\sqrt{5}+2}}{2}$ | B. | $\frac{{2\sqrt{5}+3}}{3}$ | C. | $\frac{{2\sqrt{5}}}{3}$ | D. | $\sqrt{10}$ |