题目内容
6.以直角坐标系xOy的原点为极点,x轴的非负半轴为极轴,且两坐标系取相同的长度单位.已知曲线C1的参数方程为:$\left\{\begin{array}{l}x=2cosθ\\ y=2sinθ\end{array}\right.$(θ为参数),将曲线C1上每一点的纵坐标变为原来的$\frac{1}{2}$倍(横坐标不变),得到曲线C2,直线l的极坐标方程:$\sqrt{3}ρcosθ+2ρsinθ+m=0$.(Ⅰ)求曲线C2的参数方程;
(Ⅱ)若曲线C2上的点到直线l的最大距离为$2\sqrt{7}$,求m的值.
分析 (Ⅰ)设曲线C1上一点P(x1,y1)与曲线C2上一点Q(x,y),由题知:$\left\{\begin{array}{l}x={x_1}\\ y=\frac{y_1}{2}\end{array}\right.$,由此能求出曲线C2的参数方程.
(Ⅱ) 直线l的直角坐标方程为:$\sqrt{3}x+2y+m=0$,求出曲线C2上一点B(2cosθ,sinθ)到直线l的距离,由此能求出m的值.
解答 解:(Ⅰ) 设曲线C1上一点P(x1,y1)与曲线C2上一点Q(x,y),
由题知:$\left\{\begin{array}{l}x={x_1}\\ y=\frac{y_1}{2}\end{array}\right.$,
所以$\left\{\begin{array}{l}x=2cosθ\\ y=sinθ\end{array}\right.$(θ为参数).
(Ⅱ) 由题知可得:直线l的直角坐标方程为:$\sqrt{3}x+2y+m=0$,
设曲线C2上一点B(2cosθ,sinθ)到直线l的距离为d,
则$d=\frac{{|{2\sqrt{3}cosθ+2sinθ+m}|}}{{\sqrt{7}}}=\frac{{|{4sin({θ+\frac{π}{3}})+m}|}}{{\sqrt{7}}}$,
当m>0时,${d_{max}}=\frac{4+m}{{\sqrt{7}}}=2\sqrt{7}$,解得:m=10,
当m<0时,${d_{max}}=\frac{4-m}{{\sqrt{7}}}=2\sqrt{7}$,解得:m=-10,
综上所述:m=±10.
点评 本题考查曲线的参数方程的求法,考查实数值的求法,涉及到参数方程、普通方程、极坐标方程的互化等基础知识,考查推理论证能力、运算求解能力,考查化归与转化思想、函数与方程思想,是中档题.

 名校课堂系列答案
名校课堂系列答案 已知函数f(x)的定义域为[-1,5],部分对应值如下表,f(x)的导函数y=f'(x)的图象如图所示,给出关于f(x)的下列命题:
已知函数f(x)的定义域为[-1,5],部分对应值如下表,f(x)的导函数y=f'(x)的图象如图所示,给出关于f(x)的下列命题:| x | -1 | 0 | 2 | 4 | 5 |
| f(x) | 1 | 2 | 0 | 2 | 1 |
②函数f(x)在[0,1]上是减函数,在[1,2]上是增函数;
③当1<a<2时,函数y=f(x)-a有3个零点;
④如果当x∈[-1,t]时,f(x)的最大值是2,那么t的最小值为0.
所有正确命题的序号为①④.
| A. | 1 | B. | e | C. | $\frac{1}{e}$ | D. | 0 |
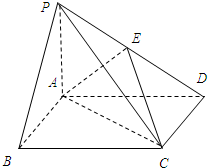 如图,四棱锥P-ABCD中,底面ABCD是矩形,PA⊥平面ABCD,PA=AB=1,BC=2,E为PD的中点.
如图,四棱锥P-ABCD中,底面ABCD是矩形,PA⊥平面ABCD,PA=AB=1,BC=2,E为PD的中点.