题目内容
已知a>0,b>0,若5
,
,5b成等比数列,则ab的最大值为 .
| a |
| 2 |
| 5 |
考点:等比数列的性质
专题:等差数列与等比数列
分析:由等比数列可得2=a+2b,结合条件由基本不等式可得.
解答:
解:∵a>0,b>0,若5
,
,5b成等比数列,
∴5=5
•5b=5
,即
=1,
∴2=a+2b≥2
,即
≤1
平方变形可得ab≤
,当且仅当a=2b=1时取等号,
故ab的最大值为:
故答案为:
| a |
| 2 |
| 5 |
∴5=5
| a |
| 2 |
| a+2b |
| 2 |
| a+2b |
| 2 |
∴2=a+2b≥2
| a•2b |
| 2ab |
平方变形可得ab≤
| 1 |
| 2 |
故ab的最大值为:
| 1 |
| 2 |
故答案为:
| 1 |
| 2 |
点评:本题考查等比数列的性质,涉及基本不等式求最值,属基础题.

练习册系列答案
 手拉手全优练考卷系列答案
手拉手全优练考卷系列答案
相关题目
函数y=
的定义域为( )
| ||
| x-1 |
| A、(-∞,2] |
| B、(-∞,2) |
| C、(-∞,1)∪(1,2] |
| D、(-∞,1)∪(1,2) |
下列函数中,定义域是R且为增函数的是( )
| A、y=x+sinx |
| B、y=e-x |
| C、y=lnx |
| D、y=|x| |
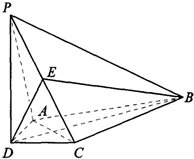 如图,在四棱锥P-ABCD中,PD⊥平面ABCD,AD⊥CD,DB平分∠ADC,E是PC的中点,AD=CD=1,
如图,在四棱锥P-ABCD中,PD⊥平面ABCD,AD⊥CD,DB平分∠ADC,E是PC的中点,AD=CD=1,