题目内容
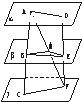
 12、如图,已知平面α、β,且α∩β=l.设梯形ABCD中,AD∥BC,且AB?α,CD?β.求证:AB,CD,l共点(相交于一点).
12、如图,已知平面α、β,且α∩β=l.设梯形ABCD中,AD∥BC,且AB?α,CD?β.求证:AB,CD,l共点(相交于一点).分析:证明线共点的问题实质上是证明点在线上的问题,其基本理论是把直线看作两平面的交线,点看作是两平面的公共点,由公理3得证.
解答:证明:∵梯形ABCD中,AD∥BC,∴AB,CD是梯形ABCD的两腰,
∴AB,CD必定相交于一点.
如图,设AB∩CD=M.
又∵AB?α,CD?β,
∴M∈α,且M∈β,
∴M∈α∩β.
又∵α∩β=l,∴M∈l,
即AB,CD,l共点
∴AB,CD必定相交于一点.
如图,设AB∩CD=M.
又∵AB?α,CD?β,
∴M∈α,且M∈β,
∴M∈α∩β.
又∵α∩β=l,∴M∈l,
即AB,CD,l共点
点评:所谓线共点问题就是证明三条或三条以上的直线交于一点.(1)证明三线共点的依据是公理3.(2)证明三线共点的思路是:先证两条直线交于一点,再证明第三条直线经过该点,把问题转化为证明点在直线上的问题.实际上,点共线、线共点的问题都可以转化为点在直线上的问题来处理.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
 如图,已知平面α∥平面β∥平面γ,且β位于α与γ之间.点A、D∈α,C、F∈γ,
如图,已知平面α∥平面β∥平面γ,且β位于α与γ之间.点A、D∈α,C、F∈γ,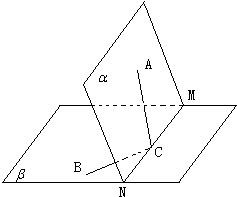 如图,已知平面α∩平面β=MN,A∈α,B∈β,C∈MN且∠ACM=60°,∠BCN=45°,二面角A-MN-B=60°,AC=2.
如图,已知平面α∩平面β=MN,A∈α,B∈β,C∈MN且∠ACM=60°,∠BCN=45°,二面角A-MN-B=60°,AC=2. (2012•青州市模拟)如图,已知平面BCC1B1是圆柱的轴截面(经过圆柱的轴的截面),BC是圆柱底面的直径,O为底面圆心,E为母线CC1的中点,已知AB=AC=AA1=4.
(2012•青州市模拟)如图,已知平面BCC1B1是圆柱的轴截面(经过圆柱的轴的截面),BC是圆柱底面的直径,O为底面圆心,E为母线CC1的中点,已知AB=AC=AA1=4. (2013•温州一模)如图,已知平面QBC与直线PA均垂直于Rt△ABC所在平面,且PA=AB=AC,
(2013•温州一模)如图,已知平面QBC与直线PA均垂直于Rt△ABC所在平面,且PA=AB=AC, (2013•宁德模拟)如图,已知平面AEMN丄平面ABCD,四边形AEMN为 正方形,四边形ABCD为直角梯形,AB∥CD,∠ABC=90°,BC=CD=2AB=2,E 为 CD 的中点.
(2013•宁德模拟)如图,已知平面AEMN丄平面ABCD,四边形AEMN为 正方形,四边形ABCD为直角梯形,AB∥CD,∠ABC=90°,BC=CD=2AB=2,E 为 CD 的中点.