Question

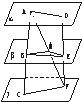如图，已知平面α∥平面β∥平面γ，且β位于α与γ之间．点A、D∈α，C、F∈γ，
AC∩β=B，DF∩β=E．
（1）求证：

AB

BC

=

DE

EF

；
（2）设AF交β于M，AC≠DF，α与β间距离为h′，α与γ间距离为h，当

h′

h

的值是多少时，△BEM的面积最大？

Answer 1

分析：（1）要证明线段对应成比例，我们可以证明①它们所在的三角形相似，也可以②利用平行线分线段成比例定理，也可以③证明它们都与同一个比例式相等，观察AB，BC，DE，EF的关系，直接证明有难度，因此可以选择第三种思路．
（2）求△BEM面积的最大值，要先将△BEM面积表示出来，再结函数的性质或基本不等式进行求解．

解答：（1）证明：连接BM、EM、BE．
∵β∥γ，平面ACF分别交β、γ于BM、CF，
∴BM∥CF．∴

AB

BC

=

AM

MF

．
同理，

AM

MF

=

DE

EF

．
∴

AB

BC

=

DE

EF

．

（2）解：由（1）知BM∥CF，
∴=

AB

AC

=

h′

h

．
同理，

ME

AD

=

h-h′

h

．
∴S_△BEM=

1

2

CF•AD

h′

h

（1-

h′

h

）sin∠BME．
据题意知，AD与CF是异面直线，只是β在α与γ间变化位置．
故CF、AD是常量，
sin∠BME是AD与CF所成角的正弦值，也是常量，
令h′：h=x．显然当x=

1

2

，即

h′

h

=

1

2

时，y=-x²+x有最大值．
∴当

h′

h

=

1

2

，即β在α、γ两平面的中间时，S_△BEM最大．

点评：要证明线段对应成比例，我们可以证明①它们所在的三角形相似，也可以②利用平行线分线段成比例定理，也可以③证明它们都与同一个比例式相等．如果已知的线段与圆的切、割有关，也可利用与圆相关的线段比例，如切线长定理、相交弦定理、切割线定理等列出线段的关系式．