题目内容
14.已知集合M={x|(x+1)(x-a)≤0}(a>0),集合N={x|-1≤x≤1},若N⊆M,则a的取值范围是( )| A. | (0,1] | B. | (0,+∞) | C. | [1,+∞) | D. | [1,2] |
分析 解不等式(x+1)(x-a)≤0可得M=[-1,a];从而利用N⊆M求得.
解答 解:∵(x+1)(x-a)≤0,
∴-1≤x≤a;
即M=[-1,a];
N={x|-1≤x≤1}=[-1,1],
∵N⊆M,
∴a的取值范围是[1,+∞);
故选C.
点评 本题考查了不等式的解法及转化思想的应用,同时考查了集合的化简与运算.

练习册系列答案
相关题目
4.设实数x,y满足约束条件$\left\{\begin{array}{l}x-2y-3≤0\\ x+2y-3≤0\\ x≥-3\end{array}\right.$,则z=-2x+3y的取值范围是( )
| A. | [-6,17] | B. | [-5,15] | C. | [-6,15] | D. | [-5,17] |
5.已知集合A={x|x2-x-2≤0},B={x|ln(1-x)>0},则A∩B=( )
| A. | (-1,2) | B. | [-1,1) | C. | [-1,0) | D. | (-1,0) |
9.其几何体的三视图如图所示(其中俯视图中的圆弧是半圆),则该几何体的表面积为( )
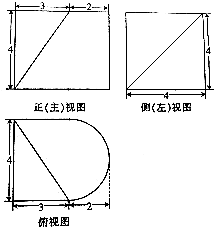

| A. | 44+2$\sqrt{34}$+8π | B. | 56+8π | C. | 44+2$\sqrt{34}$+12π | D. | 56+12π |
19.已知四个无穷数列{(-1)n$\frac{1}{n}$},{(-1)n$\frac{1}{{2}^{n}}$},{$\frac{{3}^{n-1}}{{2}^{n+2}}$},{$\frac{1{0}^{10}}{{n}^{2}}$},当n→∞时,这四个数列极限为0的个数是( )
| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
15.执行如图所示的程序框图,若输入n=6,则输出的S=( )


| A. | $\frac{1}{3}$ | B. | $\frac{2}{5}$ | C. | $\frac{3}{7}$ | D. | $\frac{4}{9}$ |