题目内容
(本题12分)直线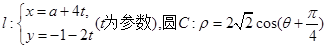 (极轴与x轴的非负半轴重合,且单位长度相同)。
(极轴与x轴的非负半轴重合,且单位长度相同)。
(1)求圆心C到直线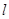 的距离; (2)若直线
的距离; (2)若直线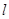 被圆C截的弦长为
被圆C截的弦长为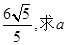 的值。
的值。
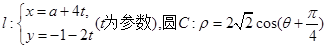 (极轴与x轴的非负半轴重合,且单位长度相同)。
(极轴与x轴的非负半轴重合,且单位长度相同)。(1)求圆心C到直线
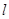 的距离; (2)若直线
的距离; (2)若直线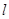 被圆C截的弦长为
被圆C截的弦长为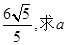 的值。
的值。(1) ;(2)
;(2) 。
。
 ;(2)
;(2) 。
。试题分析:(1)把
 化为普通方程为
化为普通方程为 ……………………2分
……………………2分把
 化为直角坐标系中的方程为
化为直角坐标系中的方程为 ……………………4分
……………………4分 圆心到直线的距离为
圆心到直线的距离为 …………………… 6分
…………………… 6分(2)由已知
 ……………………9分
……………………9分 ,
, ……………………12分
……………………12分点评:容易题,涉及参数方程、极坐标的题目,往往难度不太大,涉及圆的弦长问题,需关注弦长之半、半径、圆心到直线的距离构成的“特征三角形”。

练习册系列答案
相关题目
 时,在圆
时,在圆 上恰好有两点到直线2x+y+5=0的距离为1,则
上恰好有两点到直线2x+y+5=0的距离为1,则 的值为 。
的值为 。 和圆
和圆 的位置关系为( )
的位置关系为( )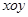 中,直线
中,直线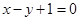 截以原点
截以原点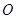 为圆心的圆所得的弦长为
为圆心的圆所得的弦长为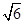
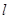 与圆
与圆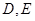 ,当
,当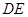 长最小时,求直线
长最小时,求直线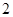 的直线
的直线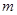 ,使
,使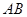 ,以
,以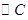 与两平行直线
与两平行直线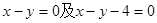 都相切,且圆心
都相切,且圆心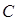 在直线
在直线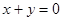 上,
上,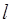 与
与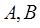 两点,
两点,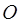 为坐标原点且满足
为坐标原点且满足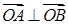 ,求直线
,求直线 为圆
为圆 的弦
的弦 的中点,则弦
的中点,则弦



 关于直线
关于直线 的对称圆方程是 .
的对称圆方程是 . 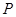 是直线
是直线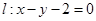 上的动点,点
上的动点,点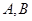 分别是圆
分别是圆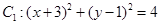 和圆
和圆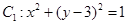 上的两个动点,则
上的两个动点,则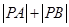 的最小值为
的最小值为