题目内容
13．“x≠1”是“x2+2x-3≠0”的（ ）| A． | 充分不必要条件 | B． | 必要不充分条件 | ||
| C． | 充要条件 | D． | 既不充分也不必要条件 |
分析 x2+2x-3≠0，解得x≠1，-3．即可判断出结论．
解答 解：x2+2x-3≠0，解得x≠1，-3．
∴“x≠1”是“x2+2x-3≠0”的必要不充分条件．
故选：B．
点评 本题考查了不等式的解法、简易逻辑的判定方法，考查了推理能力与计算能力，属于基础题．
练习册系列答案
相关题目
3．已知F是抛物线y2=4x的焦点，P1，P2，P3是该抛物线上的点，它们的横坐标依次为x1，x2，x3，若x1，x2，x3成等比数列且log2x1+log2x2+log2x3=3，则|P2F|=（ ）
| A． | 2 | B． | 3 | C． | 4 | D． | 6 |
4．已知m，n为两条不同的直线，α，β为两个不同的平面，则下列命题中正确的是（ ）
| A． | m∥n，m⊥α⇒n⊥α | B． | α∥β，m?α，n?β⇒m∥n | ||
| C． | m?α，n?β，m∥n⇒α∥β | D． | m?α，n?α，m∥β，n∥β⇒α∥β |
1．在平面直角坐标系中，已知A（1，0），B（3，2），则直线AB的倾斜角大小（ ）
| A． | 30° | B． | 45° | C． | 135° | D． | 150° |
18．
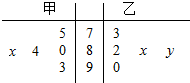在学校组织的“国学经典”朗诵比赛中，5位评委对甲、乙两名同学的评分如茎叶图所示（满分100分），若甲同学所得评分的众数为84，则甲同学所得评分的平均数不大于乙同学所得评分的平均数的概率为（ ）
在学校组织的“国学经典”朗诵比赛中，5位评委对甲、乙两名同学的评分如茎叶图所示（满分100分），若甲同学所得评分的众数为84，则甲同学所得评分的平均数不大于乙同学所得评分的平均数的概率为（ ）| A． | $\frac{3}{10}$ | B． | $\frac{1}{5}$ | C． | $\frac{7}{10}$ | D． | $\frac{4}{5}$ |