题目内容

7．函数f（x）=lg（4+3x-x2）的单调增区间为$（-1，\frac{3}{2}）$．

分析 求出函数的定义域，利用复合函数的单调性，通过求解函数y=lg（4+3x-x2）的增区间即为函数y=4+3x-x2的增区间且4+3x-x2＞0，由此即可求得．

解答 解：由4+3x-x2＞0，解得-1＜x＜4，
所以函数的定义域为（-1，4）．
函数y=lg（4+3x-x2）的增区间即为函数y=4+3x-x2的增区间且4+3x-x2＞0，
因此所求增区间为：$（-1，\frac{3}{2}）$．
故答案为：$（-1，\frac{3}{2}）$．

点评 本题考查复合函数单调性，复合函数单调性的判断方法为“同增异减”，注意函数定义域，单调区间必为定义域的子集．

练习册系列答案
相关题目
17．函数f（x）=$\frac{{\sqrt{x-1}}}{x+1}$的定义域为{x|x≥1}．
18．移动公司在互联网上就用户对某套餐服务的满意程度进行调查，参加调查的总人数为10000人，其中持各种态度的人数如表所示：
不满意一般比较满意很好
1210399826052187
移动公司为了了解用户的具体想法和意见，打算从中抽取50人进行更为详细的调查，为此要进行分层抽样，那么分层抽样时每类人中各应抽选出多少人？
15．已知数列{an}中，a1=1，an+1=2an+3（n≥2，且n∈N*）
（Ⅰ） 求证：数列{an+3}是等比数列；
（Ⅱ）求数列{an}的通项公式；
（Ⅲ）求数列{an}的前n项和Sn．
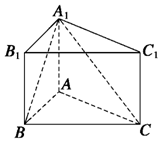2．如图，在直三棱柱ABC-A1B1C1中，AB=1，AC=AA1=$\sqrt{3}$，∠ABC=60°．
（1）证明：AB⊥A1C；
（2）（理）求二面角A-A1C-B的余弦值大小．
（文）求此棱柱的体积．
12．设集合A={x∈Z|x＞-1}，则（　　）
A．∅∉AB．$\sqrt{2}$∉AC．$\sqrt{2}∈A$D．{$\sqrt{2}$}⊆A
19．如图，菱形ABCD的边长为2，△BCD为正三角形，现将△BCD沿BD向上折起，折起后的点C记为C′，且CC′=$\sqrt{3}$，连接CC′，E为CC′的中点．
文科：（1）求证：AC′∥平面BDE；
（2）求证：CC′⊥平面BDE；
（3）求三棱锥C′-BCD的体积．
16．设函数f（x）=$\frac{1}{2}$+$\frac{1}{x}$，正项数列{an}满足a1=1，an=f（$\frac{1}{{a}_{n-1}}$），n∈N*，且n≥2．
（1）求数列{an}的通项公式；
（2）对n∈N*，求Sn=$\frac{1}{{a}_{1}{a}_{2}}$+$\frac{1}{{a}_{2}{a}_{3}}$+$\frac{1}{{a}_{3}{a}_{4}}$+…+$\frac{1}{{a}_{n}{a}_{n+1}}$．
17．某房地产开发公司计划在一楼区内建造一个长方形公园ABCD，公园由长方形的休闲区A1B1C1D1（阴影部分）和环公园人行道组成．已知休闲区A1B1C1D1的面积为4000平方米，人行道的宽分别为4米和10米．
（1）若设休闲区的长A1B1=x米，求公园ABCD所占面积S关于x的函数S（x）的解析式；
（2）要使公园所占面积最小，休闲区A1B1C1D1的长和宽该如何设计？并求出面积最小值．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网