题目内容
设函数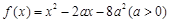 ,记不等式
,记不等式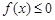 的解集为
的解集为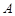 .
.
(1)当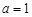 时,求集合
时,求集合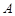 ;
;
(2)若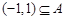 ,求实数
,求实数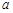 的取值范围.
的取值范围.
(1)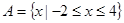 ;(2)
;(2)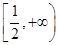 .
.
解析试题分析:(1)当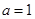 时,不等式
时,不等式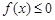 是一个具体的一元二次不等式,应用因式分解法可求得其解集;(2)注意
是一个具体的一元二次不等式,应用因式分解法可求得其解集;(2)注意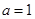 这个条件只能用于第(1)小问,而不能用于第(2)问,所以不能用第(1)小问的结果,来解第(2)问;不等式
这个条件只能用于第(1)小问,而不能用于第(2)问,所以不能用第(1)小问的结果,来解第(2)问;不等式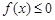
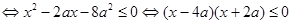 从而可得
从而可得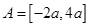 ,然后由
,然后由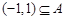 画出数轴,就可列出关于字母a的不等式组,从而求出a的取值范围.
画出数轴,就可列出关于字母a的不等式组,从而求出a的取值范围.
试题解析: (1)当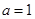 时,
时,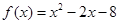 ,解不等式
,解不等式
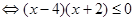 ,得
,得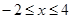 , 5分
, 5分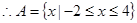 . 6 分
. 6 分
(2)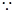
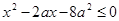 ,
,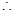
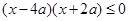 ,
,
又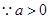 ,
,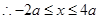 ,
,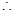
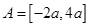 . 9分
. 9分
又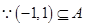 ,
, ,解得
,解得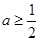 ,
,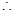 实数
实数 的取值范围是
的取值范围是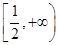 . 14分
. 14分
考点:1.一元二次不等式;2.集合间的关系.

练习册系列答案
相关题目
 ,解关于
,解关于 的不等式
的不等式 .
.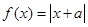 .
.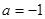 时,求不等式
时,求不等式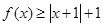 的解集;
的解集;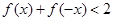 存在实数解,求实数
存在实数解,求实数 的取值范围.
的取值范围.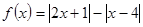 .
.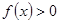 ;
; 对一切实数
对一切实数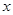 均成立,求
均成立,求 的取值范围.
的取值范围.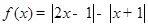 .
.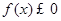 的解集
的解集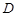 ;
;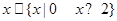 ,使得
,使得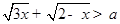 成立,求实数
成立,求实数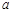 的取值范围.
的取值范围. 的不等式
的不等式 的解集为{x∣x<1或x>b}
的解集为{x∣x<1或x>b} 的值
的值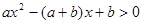
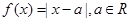
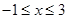 时,
时,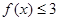 ,求a的取值范围;
,求a的取值范围;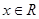 ,
,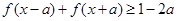 恒成立,求实数a的最小值
恒成立,求实数a的最小值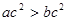 ; ②
; ②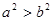 ; ③
; ③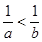 ; ④
; ④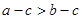 。其中正确结论的序号是 .
。其中正确结论的序号是 .  ,使得
,使得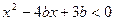 成立,则
成立,则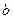 的取值范围是___▲___.
的取值范围是___▲___.