题目内容
在正四棱锥P-ABCD中,PA=2,直线PA与平面ABCD所成角为60°,E为PC的中点,则异面直线PA与BE所成角为( )
A.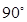 | B.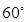  | C.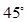 | D.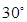 |
C
解析试题分析:连接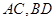 交于点
交于点 ,连接
,连接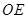 ,
,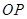 。因为
。因为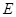 为
为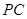 中点,所以
中点,所以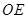 ∥
∥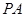 ,所以
,所以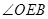 即为异面直线
即为异面直线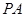 与
与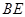 所成的角。因为四棱锥
所成的角。因为四棱锥 为正四棱锥,所以
为正四棱锥,所以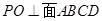 ,所以
,所以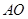 为
为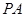 在面
在面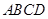 内的射影,所以
内的射影,所以 即为
即为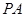 与面
与面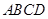 所成的角,即
所成的角,即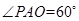 ,因为
,因为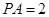 ,所以
,所以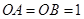 ,
, 。所以在直角三角形
。所以在直角三角形 中
中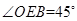 ,即面直线
,即面直线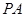 与
与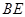 所成的角为
所成的角为 。
。
考点:1异面直线所成角;2线面角;3线面垂直。

练习册系列答案
相关题目
平面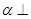 平面
平面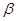 的一个充分条件是
的一个充分条件是
A.存在一条直线 , ,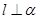 且 且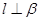 |
B.存在一个平面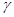 , ,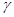 ∥ ∥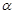 且 且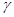 ∥ ∥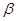 |
C.存在一个平面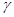 , ,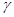 ⊥ ⊥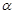 且 且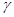 ⊥ ⊥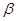 |
D.存在一条直线 , ,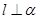 且 且 ∥ ∥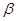 |
设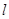 是一条直线,
是一条直线,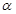 ,
,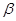 ,
,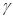 是不同的平面,则下列说法不正确的是( )
是不同的平面,则下列说法不正确的是( )
A.如果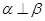 ,那么 ,那么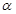 内一定存在直线平行于 内一定存在直线平行于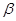 |
B.如果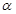 不垂直于 不垂直于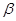 ,那么 ,那么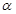 内一定不存在直线垂直于 内一定不存在直线垂直于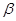 |
C.如果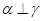 , ,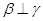 , ,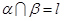 ,那么 ,那么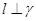 |
D.如果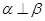 , ,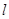 与 与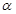 , ,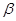 都相交,那么 都相交,那么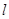 与 与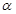 , ,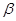 所成的角互余 所成的角互余 |
已知一个水平放置的正方形用斜二测画法作出的直观图是一个平行四边形,平行四边形中有一条边长为4,则此正方形的面积是( )
| A.16 | B.64 | C.16或64 | D.以上都不对 |
已知空间两条直线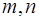 ,两个平面
,两个平面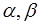 ,给出下面四个命题:
,给出下面四个命题:
①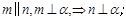 ②
②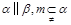 ,
,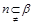
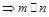 ;
;
③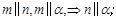 ④
④
其中正确命题的序号是( ).
| A.①④ | B.②③ | C.①②④ | D.①③④ |
如图,PA⊥正方形ABCD,下列结论中不正确的是( )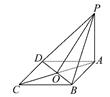
| A.PB⊥CB | B.PD⊥CD |
| C.PD⊥BD | D.PA⊥BD |
在正四面体P-ABC中,D,E,F分别是AB,BC,CA的中点,下面四个结论中不成立的( ).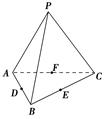
| A.BC∥平面PDF | B.DF⊥平面PAE |
| C.平面PDF⊥平面ABC | D.平面PAE⊥平面ABC |
设a,b为两条直线,α,β为两个平面,则下列结论成立的是( ).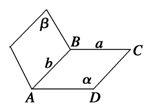
| A.若a?α,b?β,且α∩β=l,则a∥b |
| B.若a?α,b?β,且a⊥b,则α⊥β |
| C.若a∥α,b?α,则a∥b |
| D.若a⊥α,b⊥α,则a∥b |
在三棱柱ABC-A1B1C1中,各棱长相等,侧棱垂直于底面,点D是侧面BB1C1C的中心,则AD与平面BB1C1C所成角的大小是 ( ).
| A.30° | B.45° | C.60° | D.90° |