题目内容
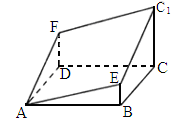
如下图所示的多面体是由底面为
ABCD的长方体被截面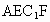
所截而得到的，其中AB=4，BC=2，
．BE=1．
(1)
求BF的长；(2)
求点C到平面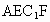的距离．
答案：略
解析：
解析：
|
解题思路： (1)过点E作EH∥BC交 于点H，则CH=BE=1，∵EH BC，∴EHAD，∴AE DH，
又∵  是长方体的截面，∴是平行四边形，
∴ AE ，∴DF ． ．
(2) 如下图，延长 、CB交于点G，连结AG，过点C作CM⊥AG交AG于点M，连结 ，过点C作 ，垂足为O，∵ ⊥平面ABCD，∴ ，
∴ AG⊥平面 ，CO 平面，∴AG⊥CO， ，AG 平面 ， 平面，
∴ CO⊥平面，
∴ CO的长即为点C到平面的距离，
∵  ，∴ ．∴ ．∴BG=1．
在△ AGB与△CMG中，∠AGC为公共角，
∴△ ABG∽△CMG，∴ ．∴ ．
而  ，∴ ．
∴  ． |
练习册系列答案
春雨教育同步作文系列答案
相关题目
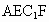所截而得到的，其中AB=4，BC=2，
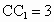，BE=1．
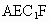的距离．
cm3
cm3
cm3
cm3
和点G的坐标;
cm3 B．
cm3 C．
cm3 D．
cm3