题目内容
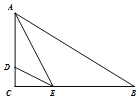
【题目】如图,在Rt△ABC中,![]() ,
,![]() ,AC=4,D在AC上且AD:DC=3:1,当∠AED最大时,△AED的面积为( )
,AC=4,D在AC上且AD:DC=3:1,当∠AED最大时,△AED的面积为( )
A.![]() B.2C.3D.
B.2C.3D.![]()
【答案】C
【解析】
根据条件得到![]() ,然后设∠AED=θ,∠AEC=α,∠DEC=β,用两角差的正切公式求出tanθ,再用基本不等式求出tanθ最大值,从而得到当∠AED最大时,△AED的面积.
,然后设∠AED=θ,∠AEC=α,∠DEC=β,用两角差的正切公式求出tanθ,再用基本不等式求出tanθ最大值,从而得到当∠AED最大时,△AED的面积.
解:因为AD:DC=3:1,所以DC![]() AC=1,
AC=1,
所以S△AED=S△ACE﹣S△DEC![]() ACCE
ACCE![]() DCEC
DCEC
![]() ACCE
ACCE![]()
![]() ACCE=ACCE(
ACCE=ACCE(![]() ACEC.
ACEC.
因为AC=4,CE≤CB,而在Rt△ABC中,![]() ,AC=4,
,AC=4,
所以CB=4![]() ,∠AED=∠AEC﹣∠DEC.
,∠AED=∠AEC﹣∠DEC.
设∠AED=θ,∠AEC=α,∠DEC=β,
则tanθ=tan(α﹣β)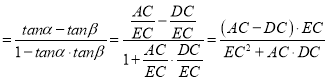
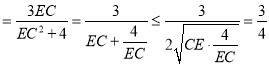 ,
,
当且仅当EC![]() ,即EC=2时,取等号,
,即EC=2时,取等号,
所以tanθ的最大值为![]() ,此时∠AED最大,
,此时∠AED最大,
所以当∠AED最大时,△AED的面积![]() =
=![]() 42=3.
42=3.
故选:C.

练习册系列答案
相关题目