题目内容
(本小题满分14分)
已知抛物线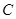 的顶点为坐标原点,焦点在
的顶点为坐标原点,焦点在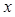 轴上. 且经过点
轴上. 且经过点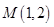 ,
,
(1)求抛物线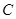 的方程;
的方程;
(2)若动直线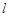 过点
过点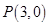 ,交抛物线
,交抛物线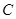 于
于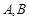 两点,是否存在垂直于
两点,是否存在垂直于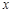 轴的直线
轴的直线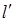 被以
被以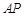 为直径的圆截得的弦长为定值?若存在,求出
为直径的圆截得的弦长为定值?若存在,求出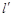 的方程;若不存在,说明理由.
的方程;若不存在,说明理由.
(1) (2)存在,
(2)存在,
解析试题分析:(1)设抛物线方程为 ,
,
将 代入方程得
代入方程得 ,
, . ……4分
. ……4分
(2)设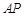 的中点为
的中点为 ,
,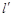 的方程为:
的方程为: ,以
,以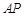 为直径的圆交
为直径的圆交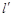 于
于 两点,
两点, 中点为
中点为 ,设
,设 , ……8分
, ……8分 ,
,

 ……12分
……12分

 .
. . ……14分
. ……14分
考点:本小题主要考查抛物线的标准方程和性质以及抛物线与直线的位置关系、弦长公式、二次函数求最值等知识,考查学生的运算求解能力和推理论证能力.
点评:圆锥曲线的题目是每年高考必考的题目,一般运算量较大,需要较强的运算能力.

练习册系列答案
相关题目
 的离心率为
的离心率为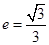 ,以原点为圆心,椭圆短半轴长为半径的圆与直线
,以原点为圆心,椭圆短半轴长为半径的圆与直线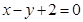 相切,
相切,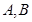 分别是椭圆的左右两个顶点,
分别是椭圆的左右两个顶点,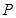 为椭圆
为椭圆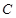 上的动点.
上的动点. 的斜率分别为
的斜率分别为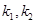 ,求
,求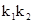 的值。
的值。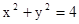 上各点的纵坐标变为原来的一半 (横坐标不变), 得到曲线
上各点的纵坐标变为原来的一半 (横坐标不变), 得到曲线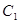 、抛物线
、抛物线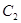 的焦点是直线y=x-1与x轴的交点.
的焦点是直线y=x-1与x轴的交点.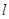 满足条件:① 过
满足条件:① 过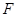 ;②与
;②与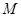 ,
,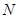 ,且满足
,且满足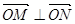 ?若存在,求出直线
?若存在,求出直线 的焦点是双曲线C的一个焦点,且双曲线经过点
的焦点是双曲线C的一个焦点,且双曲线经过点 ,又知直线
,又知直线 与双曲线C相交于A、B两点.
与双曲线C相交于A、B两点.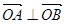 ,求实数k值.
,求实数k值.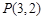 ,焦点在坐标轴上,长轴长是短轴长的3倍,求该椭圆的方程.
,焦点在坐标轴上,长轴长是短轴长的3倍,求该椭圆的方程.  (a>b>0)的离心率
(a>b>0)的离心率 ,过点
,过点 和
和 的直线与原点的距离为
的直线与原点的距离为 .
.
 ,若直线
,若直线 与椭圆交于
与椭圆交于 、
、 两 点.问:是否存在
两 点.问:是否存在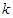 的值,
的值, 为直径的圆过
为直径的圆过 点?请说明理由.
点?请说明理由. 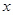 轴上,离心率为
轴上,离心率为 ,且经过点
,且经过点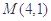 ,直线
,直线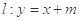 交椭圆于不同的两点
交椭圆于不同的两点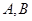 .
.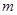 的取值范围;
的取值范围;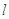 不过点
不过点 ,求证:直线
,求证:直线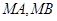 与
与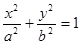 的一个焦点是
的一个焦点是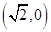 ,且截直线
,且截直线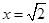 所得弦长为
所得弦长为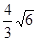 ,求该椭圆的方程.
,求该椭圆的方程.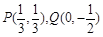 ;
;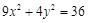 具有共同的焦点.
具有共同的焦点.