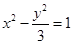题目内容
已知椭圆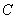 :
: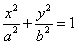 的离心率等于
的离心率等于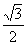 ,点
,点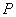
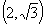 在椭圆上.
在椭圆上.
(I)求椭圆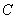 的方程;
的方程;
(Ⅱ)设椭圆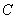 的左右顶点分别为
的左右顶点分别为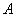 ,
,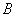 ,过点
,过点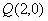 的动直线
的动直线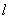 与椭圆
与椭圆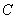 相交于
相交于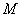 ,
,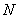 两点,是否存在定直线
两点,是否存在定直线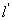 :
: ,使得
,使得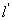 与
与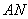 的交点
的交点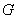 总在直线
总在直线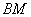 上?若存在,求出一个满足条件的
上?若存在,求出一个满足条件的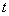 值;若不存在,说明理由。
值;若不存在,说明理由。
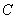 :
: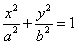 的离心率等于
的离心率等于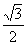 ,点
,点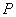
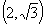 在椭圆上.
在椭圆上.(I)求椭圆
 的方程;
的方程;(Ⅱ)设椭圆
 的左右顶点分别为
的左右顶点分别为 ,
,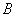 ,过点
,过点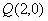 的动直线
的动直线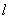 与椭圆
与椭圆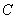 相交于
相交于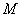 ,
,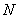 两点,是否存在定直线
两点,是否存在定直线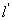 :
: ,使得
,使得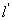 与
与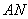 的交点
的交点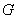 总在直线
总在直线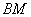 上?若存在,求出一个满足条件的
上?若存在,求出一个满足条件的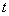 值;若不存在,说明理由。
值;若不存在,说明理由。(I)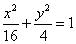
(Ⅱ) 存在定直线 :
: ,使得
,使得 与
与 的交点
的交点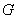 总在直线
总在直线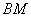 上,
上,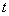 的值是
的值是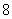 .
.
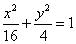
(Ⅱ) 存在定直线
 :
: ,使得
,使得 与
与 的交点
的交点 总在直线
总在直线 上,
上,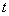 的值是
的值是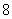 .
.试题分析:(1)由
 ,
,又点
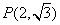 在椭圆上,
在椭圆上,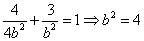 ,所以椭圆方程:
,所以椭圆方程: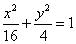 ;
; (2)当
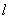 垂直
垂直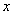 轴时,
轴时, ,则
,则 的方程是:
的方程是: ,
,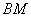 的方程是:
的方程是: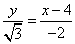 ,交点
,交点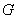 的坐标是:
的坐标是: ,猜测:存在常数
,猜测:存在常数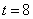 ,
,即直线
 的方程是:
的方程是: 使得
使得 与
与 的交点
的交点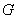 总在直线
总在直线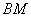 上,
上, 证明:设
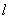 的方程是
的方程是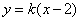 ,点
,点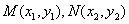 ,
,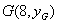
将
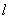 的方程代入椭圆
的方程代入椭圆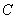 的方程得到:
的方程得到: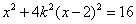 ,
,即:
 ,
, 从而:
 ,
, 因为:
 ,
,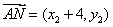
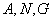 共线,所以:
共线,所以: ,
, ,
, 又
 ,
, 要证明
要证明 共线,即要证明
共线,即要证明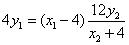 ,
, 即证明:
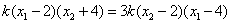 ,即:
,即: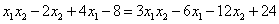 ,
,即:
 因为:
因为: 成立,
成立, 所以点
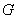 在直线
在直线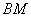 上.综上:存在定直线
上.综上:存在定直线 :
: ,使得
,使得 与
与 的交点
的交点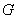 总在直线
总在直线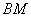 上,
上,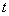 的值是
的值是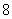 .
. 点评:本题考查椭圆方程的求法,考查满足条件的方程是否存在,综合性强,难度大,有一定的探索性,解题时要认真审题,仔细解答,注意等价转化思想的合理运用

练习册系列答案
 激活思维优加课堂系列答案
激活思维优加课堂系列答案 活力试卷系列答案
活力试卷系列答案 课课优能力培优100分系列答案
课课优能力培优100分系列答案
相关题目
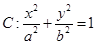 的顶点为
的顶点为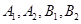 ,焦点为
,焦点为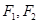 ,
,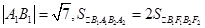 .
. 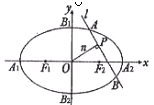
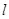 是与n垂直相交于P点,与椭圆相交于A, B两点的直线,
是与n垂直相交于P点,与椭圆相交于A, B两点的直线,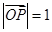 .是否存在上述直线
.是否存在上述直线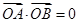 成立?若存在,求出直线
成立?若存在,求出直线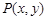 在椭圆
在椭圆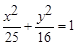 上,若
上,若 点坐标为
点坐标为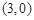 ,
, ,且
,且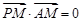 ,则
,则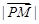 的最小值是( )
的最小值是( )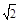
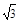

 中,若双曲线
中,若双曲线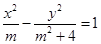 的焦距为8,则
的焦距为8,则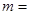
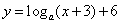 (
(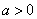 ,
,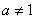 )的图象恒过定点
)的图象恒过定点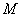 ,椭圆
,椭圆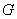 :
: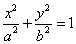 (
(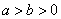 )的左,右焦点分别为
)的左,右焦点分别为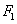 ,
,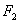 ,直线
,直线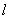 经过点
经过点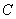 :
: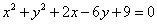 相切.
相切.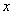 轴上方的交点为
轴上方的交点为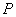 ,且
,且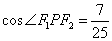 ,求
,求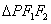 内切圆的方程.
内切圆的方程.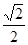 ,则
,则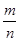 =( )
=( )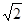 B.
B. 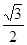 D.
D.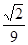
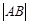 为C的实轴长的2倍,则双曲线C的离心率为( )
为C的实轴长的2倍,则双曲线C的离心率为( )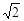
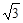
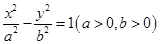 的两个焦点恰为椭圆
的两个焦点恰为椭圆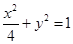 的两个顶点,且离心率为2,则该双曲线的标准方程为 ( )
的两个顶点,且离心率为2,则该双曲线的标准方程为 ( )