ĚâÄżÄÚČÝ
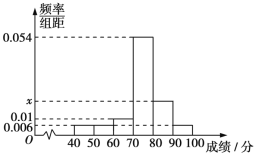
ĄžĚâÄżĄżÄł˛żĂĹÔÚÉĎ°ŕ¸ßˇĺĘąśÎśÔź×Ą˘ŇŇÁ˝×ůľŘĚúŐž¸÷ËćťúłéČĄÁË50ĂűłËżÍŁŹÍłźĆĆäłËłľľČ´ýĘąźäŁ¨Ö¸łËżÍ´Ó˝řŐžżÚľ˝łËÉĎłľľÄĘąźäŁŹľĽÎťŁşˇÖÖÓŁŠ˝ŤÍłźĆĘýžÝ°´![]() ŁŹ
ŁŹ![]() ŁŹ
ŁŹ![]() ŁŹĄŁŹ
ŁŹĄŁŹ![]() ˇÖ×飏ÖĆłÉĆľÂʡֲźÖąˇ˝ÍźČçÍźËůĘžŁş
ˇÖ×飏ÖĆłÉĆľÂʡֲźÖąˇ˝ÍźČçÍźËůĘžŁş
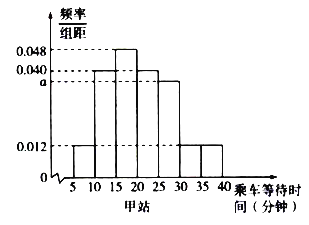
Ł¨1ŁŠÇóaľÄÖľŁť
Ł¨2ŁŠźÇAąíĘžĘÂźţĄ°ÔÚÉĎ°ŕ¸ßˇĺĘąśÎÄłłËżÍÔÚź×ŐžłËłľľČ´ýĘąźäÉŮÓÚ20ˇÖÖÓĄąĘÔšŔźĆAľÄ¸ĹÂĘŁť
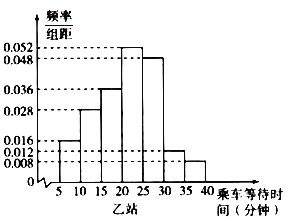
Ł¨3ŁŠźŮÉčÍŹ×éÖĐľÄĂż¸öĘýžÝÓøĂ×éÇřźä×óśËľăÖľŔ´šŔźĆŁŹźÇÔÚÉĎ°ŕ¸ßˇĺĘąśÎź×Ą˘ŇŇÁ˝Őž¸÷łéČĄľÄ50ĂűłËżÍłËłľľÄĆ˝žůľČ´ýĘąźäˇÖąđÎŞ![]() ŁŹÇó
ŁŹÇó![]() ľÄÖľŁŹ˛˘Öą˝ÓĐ´łö
ľÄÖľŁŹ˛˘Öą˝ÓĐ´łö![]() Óë
Óë![]() ľÄ´óĐĄšŘĎľ.
ľÄ´óĐĄšŘĎľ.
Ąž´đ°¸ĄżŁ¨1ŁŠ![]() Ł¨2ŁŠ0.5Ł¨3ŁŠ
Ł¨2ŁŠ0.5Ł¨3ŁŠ![]()
![]() ŁŹ
ŁŹ![]()
Ąž˝âÎöĄż
Ł¨1ŁŠ¸ůžÝĐĄł¤ˇ˝ĐÎľÄĂćťýşÍÎŞ![]() ÁС˝łĚŁŹ˝âˇ˝łĚÇóľĂ
ÁС˝łĚŁŹ˝âˇ˝łĚÇóľĂ![]() ľÄÖľ.
ľÄÖľ.
Ł¨2ŁŠ¸ůžÝĆľÂʡֲźÖąˇ˝ÍźŁŹźĆËăłöłËżÍÔÚź×ŐžľČ´ýĘąźäÉŮÓÚ20ˇÖÖÓľÄĆľÂĘŁŹÓÉ´ËšŔźĆAľÄ¸ĹÂĘ.
Ł¨3ŁŠŔűÓĂĆľÂʡֲźÖąˇ˝ÍźźĆËăłöĆ˝žůĘý![]() .¸ůžÝÍźĎóĹМϳö
.¸ůžÝÍźĎóĹМϳö![]() .
.
Ł¨1ŁŠŇňÎŞ![]() ŁŹ
ŁŹ
ËůŇÔ![]() .
.
Ł¨2ŁŠÓÉĚâŇâÖŞŁŹ¸ĂłËżÍÔÚź×ŐžľČ´ýĘąźäÉŮÓÚ20ˇÖÖÓľÄĆľÂĘÎŞ![]() ŁŹšĘ
ŁŹšĘ![]() ľÄšŔźĆ־Ϊ0.5.
ľÄšŔźĆ־Ϊ0.5.
Ł¨3ŁŠ![]()
![]() .
.
ÓÉÖąˇ˝ÍźÖŞ![]() .Ł¨ŇňÎŞŇŇÍźÖнϸ߾ÄĐĄł¤ˇ˝ĐÎÎťÓھȴýĘąźä˝Ďł¤ľÄˇśÎ§ŁŠ
.Ł¨ŇňÎŞŇŇÍźÖнϸ߾ÄĐĄł¤ˇ˝ĐÎÎťÓھȴýĘąźä˝Ďł¤ľÄˇśÎ§ŁŠ

 ÔÄśÁżěłľĎľÁĐ´đ°¸
ÔÄśÁżěłľĎľÁĐ´đ°¸