Question

【题目】已知函数．

（1）函数在内有两个不同零点，求的取值范围；

（2）在第（1）问的条件下判断当时，曲线是否位于轴下方，并说明理由．

Answer 1

【答案】（1）；（2）曲线位于轴下方，理由详见解析．

【解析】

（1）将的解析式代入，结合零点定理并分离参数可得，求得导函数后根据函数的单调性与极限值画出函数图像示意图，即可求得的取值范围；

（2）将函数变形，结合（1）中的取值范围，可知，而当时，，即可说明曲线位于轴下方.

（1）在内有两个不同零点，

∴，，

令，

则，令可解得，

当，，单调递减；

当，，单调递增

所以在取得极小值，

因为时，且，

所以的图像大致如下图所示：

所以当时，方程有两解且，，

所以．

（2）

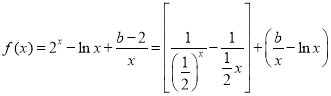
由（1）知当，，所以

当时，，所以

则，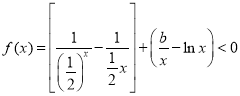

所以当时曲线位于轴下方．