题目内容
9.在菱形ABCD中,若AC=2,则$\overrightarrow{CA}$•$\overrightarrow{AB}$等于( )| A. | 2 | B. | -2 | ||
| C. | |$\overrightarrow{AB}$|cosA | D. | 与菱形的边长有关 |
分析 设对角线AC与BD交与点O,易得AC、BD互相垂直且平分,再根据$\overrightarrow{CA}$•$\overrightarrow{AB}$=-|$\overrightarrow{AC}$|•|$\overrightarrow{AB}$|•cos∠BAC=-|$\overrightarrow{AC}$|×|$\overrightarrow{AO}$|,从而得出结论.
解答 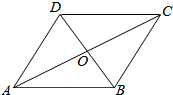 解:如图:菱形ABCD中,若AC=2,对角线AC与BD交与点O,易得AC、BD互相垂直且平分,
解:如图:菱形ABCD中,若AC=2,对角线AC与BD交与点O,易得AC、BD互相垂直且平分,
则$\overrightarrow{CA}$•$\overrightarrow{AB}$=-$\overrightarrow{AC}$•$\overrightarrow{AB}$=-|$\overrightarrow{AC}$|•|$\overrightarrow{AB}$|•cos∠BAC=-2×|$\overrightarrow{AO}$|=-2×1=-2,
故选:B.
点评 本题考查向量数量积的概念与计算,注意结合菱形的对角线的性质,属于中档题.

练习册系列答案
 备战中考寒假系列答案
备战中考寒假系列答案
相关题目
20.将函数f(x)=2sin(3x+$\frac{π}{4}$)的图象向左平移$\frac{π}{3}$个单位后得到函数y=g(x)的图象,则函数y=f(x)与函数y=g(x)的图象关于( )
| A. | x轴对称 | B. | 原点对称 | C. | y轴对称 | D. | 直线x=$\frac{π}{2}$对称 |
14.某中学将100名高一新生分成水平相同的甲、乙两个“平行班”,每班50人,陈老师采用A,B两种不同的教学方式分别在甲、乙两个班进行教改实验,为了了解教学效果,期末考试后,陈老师对甲、乙两个班级的学生成绩进行统计分析,画出频率分布直方图(如图).记成绩不低于90分者为“成绩优秀”.
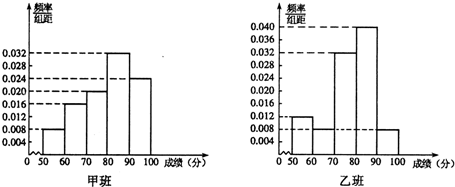
(1)从乙班随机抽取2名学生的成绩,记“成绩优秀”的个数为ξ,求ξ的分布列和数学期望;
(2)根据频率分布直方图填写下面2×2列联表,并判断能否在犯错误的概率不超过0.05的前提下认为:“成绩优秀”与教学方式有关.
附:${K^2}=\frac{{n{{(ad-bc)}^2}}}{(a+b)(c+d)(a+c)(b+d)}$.

(1)从乙班随机抽取2名学生的成绩,记“成绩优秀”的个数为ξ,求ξ的分布列和数学期望;
(2)根据频率分布直方图填写下面2×2列联表,并判断能否在犯错误的概率不超过0.05的前提下认为:“成绩优秀”与教学方式有关.
| 甲班(A方式) | 乙班(B方式) | 总计 | |
| 成绩优秀 | |||
| 成绩不优秀 | |||
| 总计 |
| P(K2≥k) | 0.25 | 0.15 | 0.10 | 0.05 | 0.025 |
| k | 1.323 | 2.072 | 2.706 | 3.841 | 5.024 |
18.已知数列{an}的前n项和Sn=k-kan(a,k都是不为0的常数)是数列{an}为等比数列的( )
| A. | 充分非必要条件 | B. | 必要非充分条件 | ||
| C. | 充要条件 | D. | 既不充分又不必要条件 |
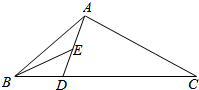 如图,在△ABC中,AB=AC=1,cos∠BAC=$\frac{1}{3}$,D是BC上一点,且DC=2BD,E是AD的中点,则BE的长为$\frac{\sqrt{129}}{18}$.
如图,在△ABC中,AB=AC=1,cos∠BAC=$\frac{1}{3}$,D是BC上一点,且DC=2BD,E是AD的中点,则BE的长为$\frac{\sqrt{129}}{18}$.