题目内容
17.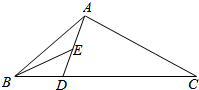 如图,在△ABC中,AB=AC=1,cos∠BAC=$\frac{1}{3}$,D是BC上一点,且DC=2BD,E是AD的中点,则BE的长为$\frac{\sqrt{129}}{18}$.
如图,在△ABC中,AB=AC=1,cos∠BAC=$\frac{1}{3}$,D是BC上一点,且DC=2BD,E是AD的中点,则BE的长为$\frac{\sqrt{129}}{18}$.
分析 求出AD,BD,利用平行四边形对角线的平方的和等于四条边的平方和,可得结论.
解答 解:∵△ABC中,AB=AC=1,cos∠BAC=$\frac{1}{3}$,
∴BC=$\sqrt{1+1-2×1×1×\frac{1}{3}}$=$\frac{2\sqrt{3}}{3}$,
∵DC=2BD,
∴DC=$\frac{4\sqrt{3}}{9}$,BD=$\frac{2\sqrt{3}}{9}$
∵$\frac{1}{sinC}=\frac{\frac{2\sqrt{3}}{3}}{\frac{2\sqrt{2}}{3}}$,
∴sinC=$\frac{\sqrt{6}}{3}$,
∴cosC=$\frac{\sqrt{3}}{3}$,
∴AD2=1+$\frac{48}{81}$-2×1×$\frac{4\sqrt{3}}{9}$×$\frac{\sqrt{3}}{3}$=$\frac{57}{81}$,
∴2[1+($\frac{2\sqrt{3}}{9}$)2]=$\frac{57}{81}$+(2BE)2,
∴BE=$\frac{\sqrt{129}}{18}$.
故答案为:$\frac{\sqrt{129}}{18}$.
点评 本题考查正弦定理、余弦定理的运用,考查学生的计算能力,利用平行四边形对角线的平方的和等于四条边的平方和是关键.

练习册系列答案
相关题目
8.若实数x,y满足不等式组$\left\{\begin{array}{l}{x+3y-3≥0}\\{2x-y-3≤0}\\{x-my+1≥0}\end{array}\right.$,且x+y的最大值为4,则实数m=( )
| A. | -1 | B. | 0 | C. | 1 | D. | 2 |
9.在菱形ABCD中,若AC=2,则$\overrightarrow{CA}$•$\overrightarrow{AB}$等于( )
| A. | 2 | B. | -2 | ||
| C. | |$\overrightarrow{AB}$|cosA | D. | 与菱形的边长有关 |
7.已知某种产品的数量x(件)与其成本y(元)之间的函数关系可以近似用y=ax2+bx+c表示,其中a、b、c为待定常数,现有实际统计数据如下表:
(1)试确定成本函数y=f(x);
(2)已知这种产品每件的销售价为200元,求利润p关于x的函数p=p(x);
(3)根据利润p关于x的函数p=p(x)确定盈亏转折时的产品数量(即产品数量等于多少时,能扭亏为盈或由盈转亏).
| 产品数量x(件) | 6 | 10 | 20 |
| 成本合计y(元) | 1040 | 1600 | 3700 |
(2)已知这种产品每件的销售价为200元,求利润p关于x的函数p=p(x);
(3)根据利润p关于x的函数p=p(x)确定盈亏转折时的产品数量(即产品数量等于多少时,能扭亏为盈或由盈转亏).




