题目内容
 一个空间几何体
一个空间几何体![]() 的三视图如图所 示,其中
的三视图如图所 示,其中![]() 分别是
分别是![]() 五点在直立、侧立、水平三个投影面内的投影,且在主视图中,四边形
五点在直立、侧立、水平三个投影面内的投影,且在主视图中,四边形![]() 为正方形且
为正方形且![]() ;在左视图中
;在左视图中![]() 俯视图中
俯视图中![]() ,
,
(Ⅰ)根据三视图作出空间几何体![]() 的直观图,并标明
的直观图,并标明![]() 五点的位置;
五点的位置;
(Ⅱ)在空间几何体![]() 中,过点
中,过点![]() 作平面
作平面![]() 的垂线,若垂足H在直线
的垂线,若垂足H在直线![]() 上,求证:平面
上,求证:平面![]() ⊥平面
⊥平面![]() ;
;
(Ⅲ)在(Ⅱ)的条件下,求三棱锥![]() 的体积及其外接球的表面积.
的体积及其外接球的表面积.
平面![]() ⊥平面
⊥平面![]()
解析:
(Ⅰ)空间几何体的直观图如图所示,
且可得到平面![]() ⊥平面
⊥平面![]() ,
,
 四边形
四边形![]() 为正方形且
为正方形且![]()
(Ⅱ)证明:![]() 过点
过点![]() 作平面
作平面![]() 的垂线,
的垂线,
垂足H在直线![]() 上,
上,
![]() 平面
平面![]() ,
,
![]() 平面
平面![]() ,
,![]() ,
,
又![]() 平面
平面![]()
![]() ⊥平面
⊥平面![]() ,
,
又![]() ,故平面
,故平面![]() ⊥平面
⊥平面![]()
(Ⅲ)由(Ⅱ)知,![]() ,
,
![]()
![]() 为等腰直角三角形,
为等腰直角三角形,
过点![]() 作
作![]() 于点
于点![]() ,则
,则![]() ,
,
![]()
∴![]()
取![]() 的中点
的中点![]() ,由于
,由于![]() 均为直角三角形,所以
均为直角三角形,所以
![]()
![]()
![]() 是四棱锥
是四棱锥![]() 的外接球的球心,半径为
的外接球的球心,半径为![]()
![]()

练习册系列答案
相关题目
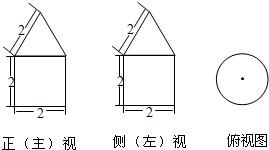 一个空间几何体的三视图如图所示,则该几何体的体积为( )
一个空间几何体的三视图如图所示,则该几何体的体积为( )A、2π+
| ||||
B、
| ||||
C、2π+
| ||||
D、4π+
|
一个空间几何体的三视图如图所示,则该几何体的表面积为( )
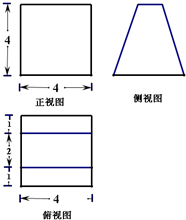

| A、48 | ||
B、32+8
| ||
C、48+8
| ||
| D、80 |
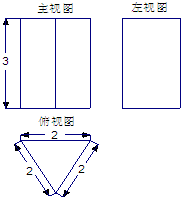 已知一个空间几何体的三视图如图所示,根据图中标出的尺寸,可得这个几何体的表面积是
已知一个空间几何体的三视图如图所示,根据图中标出的尺寸,可得这个几何体的表面积是 已知一个空间几何体的三视图如图所示,主视图、侧视图是斜边长为
已知一个空间几何体的三视图如图所示,主视图、侧视图是斜边长为 已知一个空间几何体的三视图如图所示,则这个几何体的表面积是
已知一个空间几何体的三视图如图所示,则这个几何体的表面积是