Question

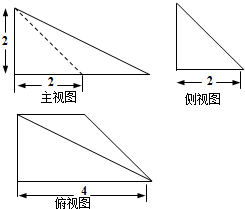
已知一个空间几何体的三视图如图所示，主视图、侧视图是斜边长为

2

的等腰直角三角形，该几何体的体积是（　　）

• A．

  1

  3

• B．

  2

  3

• C．

  3

  3

• D．

  2

  3

Answer 1

分析：几何体是一个四棱锥，四棱锥的底面是一个边长为

2

正方形，侧视图是一个斜边长为

2

的等腰直角三角形，做出四棱锥的高是

2

2

，根据四棱锥的体积公式写出体积．

解答：解：由三视图知几何体是一个四棱锥，
四棱锥的底面是一个边长为

2

正方形，
侧视图是一个斜边长为

2

的等腰直角三角形，
∴四棱锥的高是

2

2

，
∴四棱锥的体积是

1

3

×

2

×

2

×

2

2

=

2

3

故选B．

点评：本题考查由三视图还原几何体且求几何体的体积，本题解题的关键是有三视图看出几何体的结构和各个部分的长度，特别是本图中四棱锥的高度长度容易出错．