题目内容
设数列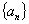 的前
的前 项和为
项和为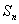 ,对任意的正整数
,对任意的正整数 ,都有
,都有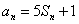 成立,记
成立,记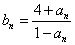 .(1)求数列
.(1)求数列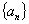 与数列
与数列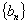 的通项公式;
的通项公式;
(2)设数列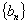 的前
的前 项和为
项和为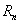 ,是否存在正整数
,是否存在正整数 ,使得
,使得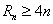 成立?若存在,找出一个正整数
成立?若存在,找出一个正整数 ;若不存在,请说明理由.
;若不存在,请说明理由.
(3)记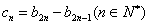 ,设数列
,设数列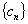 的前
的前 项和为
项和为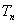 ,求证:对于
,求证:对于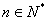 都有
都有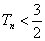
解:(1)当 时,
时,
又

∴数列 是首项为
是首项为 ,公比为
,公比为 的等比数列,
的等比数列,
∴ ,
,
(2)不存在正整数 ,使得
,使得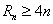 成立。
成立。
证明:由(1)知

∴当n为偶数时,设
∴
当n为奇数时,设
∴
∴对于一切的正整数n,都有
∴不存在正整数 ,使得
,使得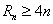 成立。
成立。
(3)由 得
得


|

练习册系列答案
相关题目

 则数列{ an}的公比为q为( )
则数列{ an}的公比为q为( ) 的焦点为顶点,以椭圆
的焦点为顶点,以椭圆 的顶点为焦点的双曲线的方程是
的顶点为焦点的双曲线的方程是 B、
B、 C、
C、 D、
D、
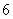 个面的中心,甲从这
个面的中心,甲从这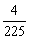 B.
B. 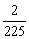 C.
C. 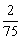 D.
D. 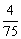
 ,
, ,
, ,则向量
,则向量 与向量
与向量 的夹角是
的夹角是 B.
B. C.
C. D.
D.
 ,3) D.(5,9)
,3) D.(5,9)