题目内容
已知向量a = ,b=
,b= ,设函数
,设函数 =a
=a b.
b.
(Ⅰ)求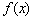 的单调递增区间;
的单调递增区间;
(Ⅱ)若将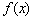 的图象向左平移
的图象向左平移 个单位,得到函数
个单位,得到函数 的图象,求函数
的图象,求函数 在区间
在区间 上的最大值和最小值.
上的最大值和最小值.
解:(Ⅰ) f(x)=a•b=2sin2x+2sinxcosx
= +sin2x
+sin2x
= sin(2x-
sin(2x- )+1,
)+1,
由- +2kπ≤2x-
+2kπ≤2x- ≤
≤ +2kπ,k∈Z,得-
+2kπ,k∈Z,得- +kπ≤x≤
+kπ≤x≤ +kπ,k∈Z,
+kπ,k∈Z,
∴ f(x)的单调递增区间是[- +kπ,
+kπ, +kπ]( k∈Z).
+kπ]( k∈Z).
(II)由题意g(x)= sin[2(x+
sin[2(x+ )-
)- ]+1=
]+1= sin(2x+
sin(2x+ )+1,
)+1,
由 ≤x≤
≤x≤ 得
得 ≤2x+
≤2x+ ≤
≤ ,
,
∴ 0≤g(x)≤ +1,即 g(x)的最大值为
+1,即 g(x)的最大值为 +1,g(x)的最小值为0.
+1,g(x)的最小值为0.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
 ,则直线
,则直线 的倾斜角的取值范围是 。
的倾斜角的取值范围是 。 ,若点
,若点 为平面区域
为平面区域 上的一个动点,则|AM|的最小值是
上的一个动点,则|AM|的最小值是 B.
B. C.
C. D.
D.

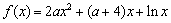 .
.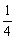 处的切线与直线4x+y=0平行,求a的值;
处的切线与直线4x+y=0平行,求a的值;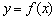 的图象与x轴交于A,B两点,线段AB中点的横坐标为
的图象与x轴交于A,B两点,线段AB中点的横坐标为 ,证明
,证明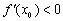 .
. 上,且点P到x轴的距离与点P到此抛物线的焦点的距离之比为
上,且点P到x轴的距离与点P到此抛物线的焦点的距离之比为 ,则点P到x轴的距离是
,则点P到x轴的距离是 (B)
(B) (C)1 (D)2
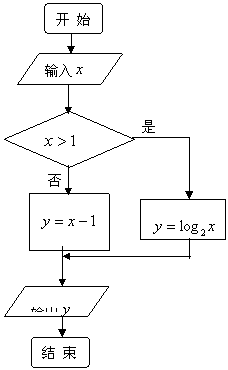
(C)1 (D)2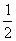 ,则输入的实数
,则输入的实数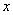 的值是
的值是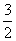 B.
B. 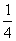 C.
C. 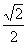 D.
D. 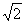
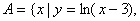
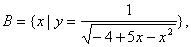 则
则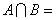 ( )
( )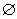 B.
B. C.
C.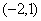 D.
D.