题目内容
(本小题满分13分)
已知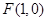 ,
, 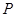 是平面上一动点,
是平面上一动点, 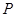 到直线
到直线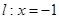 上的射影为点
上的射影为点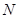 ,且满足
,且满足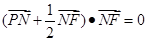
(Ⅰ)求点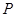 的轨迹
的轨迹 的方程;
的方程;
(Ⅱ)过点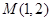 作曲线
作曲线 的两条弦
的两条弦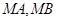 , 设
, 设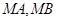 所在直线的斜率分别为
所在直线的斜率分别为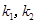 , 当
, 当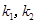 变化且满足
变化且满足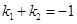 时,证明直线
时,证明直线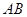 恒过定点,并求出该定点坐标.
恒过定点,并求出该定点坐标.
已知
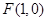 ,
, 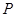 是平面上一动点,
是平面上一动点, 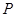 到直线
到直线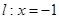 上的射影为点
上的射影为点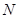 ,且满足
,且满足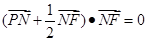
(Ⅰ)求点
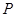 的轨迹
的轨迹 的方程;
的方程;(Ⅱ)过点
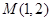 作曲线
作曲线 的两条弦
的两条弦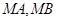 , 设
, 设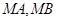 所在直线的斜率分别为
所在直线的斜率分别为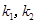 , 当
, 当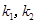 变化且满足
变化且满足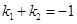 时,证明直线
时,证明直线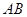 恒过定点,并求出该定点坐标.
恒过定点,并求出该定点坐标.(1) y2="4x" (2) 直线AB经过(5,-6)这个定点
试题分析:解: (Ⅰ)设曲线C上任意一点P(x,y), 又F(1,0),N(-1,y),从而

 ,
, ,
,
化简得y2="4x," 即为所求的P点的轨迹C的对应的方程. ………………4分
(Ⅱ)设
 、
、 、
、 、
、
将MB与
 联立,得:
联立,得:
∴
 ①
①同理
 ②
②而AB直线方程为:
 ,即
,即 ③
③………………8分
由①②:y1+y2=

代入③,整理得
 恒成立………………10分
恒成立………………10分则
 故直线AB经过(5,-6)这个定点.. ………………13分
故直线AB经过(5,-6)这个定点.. ………………13分点评:解决该试题的关键是利用设点,得到关系式,然后坐标化,进而化简得到轨迹方程。属于基础题。

练习册系列答案
相关题目

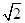
 ,且向量
,且向量 与
与 垂直,则实数
垂直,则实数 的值是 .
的值是 . 满足则
满足则 ,则
,则 。
。 中,
中, 为中线
为中线 上的一个动点,若
上的一个动点,若 ,则
,则 的最小值为 .
的最小值为 .  ,则
,则 在
在 方向上的投影为( )
方向上的投影为( )


 ,
, 满足
满足 ,且
,且 ,则
,则 .
. 则
则 的值为 ( )
的值为 ( )



 ,且
,且 ,则
,则 的取值范围是( )
的取值范围是( )


