题目内容
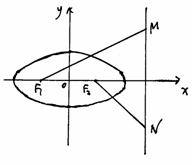
如图，椭圆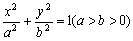
过点P(1, 
)，其左、右焦点分别为F1,F2,离心率e＝
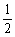, M, N是直线x＝4上的两个动点，且
·
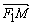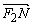＝0.
（1）求椭圆的方程；
（2）求MN的最小值；
（3）以MN为直径的圆C是否过定点？请证明你的结论。
解：（1）由已知可得
∴椭圆的方程为
＝1
（2）设M（4，m），N（4，n），∵F1(－1，0)，F2(1，0)
＝(5，m)，
＝(3，n)，由
＝0mn＝－15＜0 …
∴|MN|＝|m－n|＝|m|＋|n|＝|m|＋
≥2
∴|MN|的最小值为2
（3）以MN为直径的圆C的方程为：(x－4)2＋(y－
)＝(
)2
令y＝0得(x－4)2＝
－
＝－mn＝15x＝4±
所以圆C过定点(4－，0)和(4＋，0)
练习册系列答案
津桥教育计算小状元系列答案
相关题目
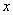的方程
有实根，则
的取值范围是________．
的两条渐近线将平面划分为“上、下、左、右”四个区域（不含边界），若点(1, 2)在“上”区域内，则双曲线离心率的取值范围为 。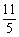
D．
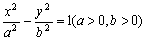的左焦点为F1，左、右顶点分别为A1、A2，
则f′（x）
的解集为 （ ）
B．（-1,0）
C．
D．