题目内容
由直线 上的点向圆(x-4)2+(y+2)2=1引切线,则切线长的最小值为
上的点向圆(x-4)2+(y+2)2=1引切线,则切线长的最小值为
 上的点向圆(x-4)2+(y+2)2=1引切线,则切线长的最小值为
上的点向圆(x-4)2+(y+2)2=1引切线,则切线长的最小值为A. | B. | C. | D. |
B
分析:要使切线长最小,必须直线y=x+2上的点到圆心的距离最小,此最小值即为圆心(4,-2)到直线的距离m,
求出m,由勾股定理可求切线长的最小值.
解答:解:要使切线长最小,必须直线y=x+2上的点到圆心的距离最小,此最小值即为圆心(4,-2)到直线的距离m,
由点到直线的距离公式得 m= =4
=4 ,
,
由勾股定理求得切线长的最小值为 =
= =
= .
.
故选 B.
求出m,由勾股定理可求切线长的最小值.
解答:解:要使切线长最小,必须直线y=x+2上的点到圆心的距离最小,此最小值即为圆心(4,-2)到直线的距离m,
由点到直线的距离公式得 m=
 =4
=4 ,
,由勾股定理求得切线长的最小值为
 =
= =
= .
.故选 B.

练习册系列答案
相关题目
 :
:  ,圆C:
,圆C:  .
. 到点F的距离比它到直线
到点F的距离比它到直线 轴交于点O、A,与y轴交于点O、B,其中O为原点.(1)求证:△OAB的面积为定值;(2)设直线y = –2x+4与圆C交于点M, N,若OM = ON,求t的值并求出圆C的方程.
轴交于点O、A,与y轴交于点O、B,其中O为原点.(1)求证:△OAB的面积为定值;(2)设直线y = –2x+4与圆C交于点M, N,若OM = ON,求t的值并求出圆C的方程.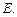
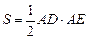 ,求
,求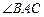 的大小.
的大小.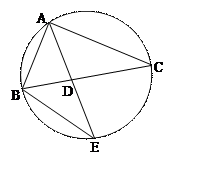
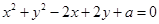 表示圆,则实数
表示圆,则实数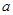 的取值范围是( )
的取值范围是( )



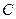 和
和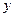 轴相切,圆心在直线
轴相切,圆心在直线 上,且被直线
上,且被直线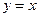 截得的弦长为
截得的弦长为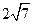 ,求圆
,求圆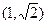 的直线l将圆
的直线l将圆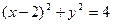 分成两段弧,当劣弧所对的圆心角最小时,求直线l的斜率。
分成两段弧,当劣弧所对的圆心角最小时,求直线l的斜率。 +
+ -4x=0外一点P(m,n)作圆的两条切线,当这两条切线互相垂直时,m,n 应满足的关系式为( )
-4x=0外一点P(m,n)作圆的两条切线,当这两条切线互相垂直时,m,n 应满足的关系式为( ) +
+  ="4"
="4"  +
+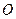 与
与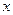 轴的正半轴的交点为
轴的正半轴的交点为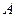 ,点
,点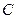 、
、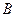 在圆
在圆
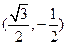 ,
,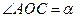 .
.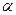 表示);
表示);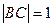 ,求
,求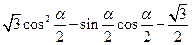 的值.
的值.