题目内容
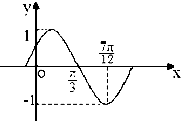
函数y=Asinωxcosωx(A>0,ω>0)的最小正周期是π,最大值是2,则函数f(x)=2sin(ωx+
)的一个单调递增区间是( )
| π |
| A |
A.[-
| B.[-
| C.[
| D.[
|
∵y=Asinωxcosωx=
Asin2ωx的最小正周期是π,最大值是2,
∴ω=1,A=4,
∴f(x)=2sin(x+
),
由2kπ-
≤x+
≤2kπ+
(k∈Z)得:
2kπ-
≤x≤2kπ+
(k∈Z),
令k=1,可得f(x)=2sin(x+
)的一个单调递增区间是[
,
].
故选D.
| 1 |
| 2 |
∴ω=1,A=4,
∴f(x)=2sin(x+
| π |
| 4 |
由2kπ-
| π |
| 2 |
| π |
| 4 |
| π |
| 2 |
2kπ-
| 3π |
| 4 |
| π |
| 4 |
令k=1,可得f(x)=2sin(x+
| π |
| 4 |
| 5π |
| 4 |
| 9π |
| 4 |
故选D.

练习册系列答案
 智趣寒假作业云南科技出版社系列答案
智趣寒假作业云南科技出版社系列答案
相关题目
 把函数
把函数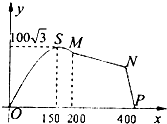 如图,顺达架校拟在长为400m的道路OP的一侧修建一条训练道路,训练道路的前一部分为曲线段OSM,该曲线段为函数y=Asinωx(A>0,ω>0),x∈[0,200]的图象,且图象的最高点为
如图,顺达架校拟在长为400m的道路OP的一侧修建一条训练道路,训练道路的前一部分为曲线段OSM,该曲线段为函数y=Asinωx(A>0,ω>0),x∈[0,200]的图象,且图象的最高点为 如图,成都市准备在南湖的一侧修建一条直路EF,另一侧修建一条观光大道,大道的前一部分为曲线段FBC,该曲线段是函数
如图,成都市准备在南湖的一侧修建一条直路EF,另一侧修建一条观光大道,大道的前一部分为曲线段FBC,该曲线段是函数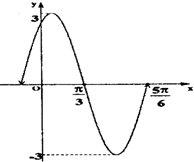 函数
函数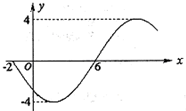 函数
函数