题目内容
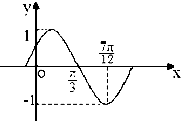 把函数y=Asin(ωx+?)(ω>0,|?|<
把函数y=Asin(ωx+?)(ω>0,|?|<| π |
| 2 |
| π |
| 3 |
分析:根据函数图象平移后,函数f(x)的最值不变,得A=1,而且周期也不变,T=4(
-
)=π,得到ω=2.最后根据函数的最小值为f(
)=-1加以讨论,即可算出φ=-
.
| 7π |
| 12 |
| π |
| 3 |
| 11π |
| 12 |
| π |
| 3 |
解答:解:由题意,得y=f(x)=Asin[ω(x+
)+φ]
∵f(x)的最大值为1,∴A=1
图象平移后,函数f(x)的周期和最值不变
得函数的周期T满足:
T=
-
=
∴周期T=
=π,得ω=2
∵当x=
+
=
时,函数有最小值为-1
∴2(
+
)+φ=-
+2kπ,k∈Z
结合|φ|≤
,取k=1得φ=-
故选:C
| π |
| 3 |
∵f(x)的最大值为1,∴A=1
图象平移后,函数f(x)的周期和最值不变
得函数的周期T满足:
| 1 |
| 4 |
| 7π |
| 12 |
| π |
| 3 |
| π |
| 4 |
∴周期T=
| 2π |
| ω |
∵当x=
| 7π |
| 12 |
| π |
| 3 |
| 11π |
| 12 |
∴2(
| 11π |
| 12 |
| π |
| 3 |
| π |
| 2 |
结合|φ|≤
| π |
| 2 |
| π |
| 3 |
故选:C
点评:本题给出三角函数的图象,求参数φ的值,着重考查了三角函数的周期性和三角函数y=Asin(ωx+φ)的图象变换等知识,属于基础题.

练习册系列答案
相关题目
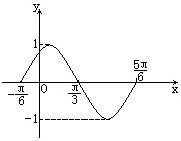 如图是函数y=Asin(ωx+φ)(A<0,ω>0,|φ|≤
如图是函数y=Asin(ωx+φ)(A<0,ω>0,|φ|≤| π |
| 2 |
A、向左平移
| ||||
B、向左平移
| ||||
C、向左平移
| ||||
D、向左平移
|
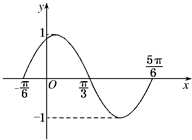 图是函数y=Asin(ωx+φ)(x∈R)在区间[-
图是函数y=Asin(ωx+φ)(x∈R)在区间[-| π |
| 6 |
| 5π |
| 6 |
A、向左平移
| ||||
B、向左平移
| ||||
C、向左平移
| ||||
D、向左平移
|
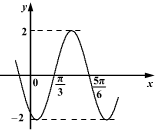 函数y=Asin(ωx+φ)(A>0,ω>0)的图象一部分如图所示,则要得到该函数的图象,只需将函数f(x)=2sinx的图象.( )
函数y=Asin(ωx+φ)(A>0,ω>0)的图象一部分如图所示,则要得到该函数的图象,只需将函数f(x)=2sinx的图象.( )