题目内容
在平面直角坐标系xoy中,已知椭圆的焦点为(-
,0)(
,0),离心率为
.
(1)求椭圆的方程;
(2)若圆M:x2+(y-m)2=1上的点到椭圆上的点的最远距离为
+1,求m的值;
(3)过坐标原点作斜率为k的直线l交椭圆于P、Q两点,点N为椭圆上任意一点(异于点P,Q),设直线NP,NQ的斜率均存在且分别记为kNp,kNQ.证明:对任意k,恒有kNPkNQ=-
.
| 3 |
| 3 |
| ||
| 2 |
(1)求椭圆的方程;
(2)若圆M:x2+(y-m)2=1上的点到椭圆上的点的最远距离为
| 5 |
(3)过坐标原点作斜率为k的直线l交椭圆于P、Q两点,点N为椭圆上任意一点(异于点P,Q),设直线NP,NQ的斜率均存在且分别记为kNp,kNQ.证明:对任意k,恒有kNPkNQ=-
| 1 |
| 4 |
考点:直线与圆锥曲线的综合问题
专题:圆锥曲线中的最值与范围问题
分析:(1)由题意得
,由此能求出椭圆方程.
(2)原题转化为求MT取最大值实数m的求解,设T(x,y),则MT2=x2+(y-m)2=-3y2-2my+m2+4(-1≤y≤1),由此利用分类讨论思想能求出m的值.
(3)由已知得kNP•kNQ=
•
=
,由此能证明对任意k,恒有kNPkNQ=-
.
|
(2)原题转化为求MT取最大值实数m的求解,设T(x,y),则MT2=x2+(y-m)2=-3y2-2my+m2+4(-1≤y≤1),由此利用分类讨论思想能求出m的值.
(3)由已知得kNP•kNQ=
| y1-y0 |
| x1-x0 |
| y1+y0 |
| x1+x2 |
| y12-y02 |
| x12-x02 |
| 1 |
| 4 |
解答:
(1)解:由题意得
,
解得a=2,b=1,
∴椭圆方程为
+y2=1.
(2)解:设圆M上任取一点S,椭圆上任取一点T,则ST≤MT+MS=MT+1,
故转化为求圆心M到椭圆上点T的距离的最大值,即MT的最大值,
设T(x,y),则MT2=x2+(y-m)2,
又∵点T在椭圆上,∴
+y2=1,
∴MT2=x2+(y-m)2=-3y2-2my+m2+4(-1≤y≤1),
当-
≤1,即m≥3,此时y=-1,
MT2取到最大值为m2+2m+1,
∴(m+1)2=5,解得m=-1±
∉[3,+∞),舍去,
当-
≥1,即m≤-3时,此时y=1,MT2取到最大值为m2-2m+1,
∴(m-1)2=5,解得m=1±
∉(-∞,-3],舍去,
当-1<-
<1,即-3<m<3时,y=-
,
MT2取到最大值为
m2+4,
∴
m2+4=5,解得m=±
∈(-3,3),符合题意,
∴m的值为±
.
(3)证明:根据题意知P,Q关于原点对称,
∴kNP=
,kNQ=
,
∴kNP•kNQ=
•
=
,
又点P,N在椭圆上,
∴
,
两式相减,得
=-
,
∴对任意k,恒有kNPkNQ=-
.
|
解得a=2,b=1,
∴椭圆方程为
| x2 |
| 4 |
(2)解:设圆M上任取一点S,椭圆上任取一点T,则ST≤MT+MS=MT+1,
故转化为求圆心M到椭圆上点T的距离的最大值,即MT的最大值,
设T(x,y),则MT2=x2+(y-m)2,
又∵点T在椭圆上,∴
| x2 |
| 4 |
∴MT2=x2+(y-m)2=-3y2-2my+m2+4(-1≤y≤1),
当-
| m |
| 3 |
MT2取到最大值为m2+2m+1,
∴(m+1)2=5,解得m=-1±
| 5 |
当-
| m |
| 3 |
∴(m-1)2=5,解得m=1±
| 5 |
当-1<-
| m |
| 3 |
| m |
| 3 |
MT2取到最大值为
| 4 |
| 3 |
∴
| 4 |
| 3 |
| ||
| 2 |
∴m的值为±
| ||
| 2 |
(3)证明:根据题意知P,Q关于原点对称,
∴kNP=
| y1-y0 |
| x1-x0 |
| y1+y0 |
| x1+x0 |
∴kNP•kNQ=
| y1-y0 |
| x1-x0 |
| y1+y0 |
| x1+x2 |
| y12-y02 |
| x12-x02 |
又点P,N在椭圆上,
∴
|
两式相减,得
| y12-y02 |
| x12-x02 |
| 1 |
| 4 |
∴对任意k,恒有kNPkNQ=-
| 1 |
| 4 |
点评:本题考查椭圆方程的求法,考查满足条件的实数值的求法,考查直线的斜率之积为定值的证明,解题时要认真审题,注意函数与方程思想的合理运用.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
执行如图所示的程序框图,若输出的s的值是100,则框图中的n的值是( )


| A、3 | B、4 | C、5 | D、6 |
函数f(x)=log2x-
+a的一个零点在(1,4)内,则实数a的取值范围为( )
| 2 |
| x |
A、(-
| ||
| B、(4,6) | ||
| C、(2,4) | ||
D、(-3,-
|
已知a,b,c满足c<b<a且ac<0,则下列选项中不一定能成立的是( )
A、
| ||||
B、
| ||||
C、
| ||||
D、
|
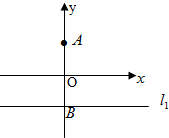 已知定点A(0,a)(a>0),直线l1:y=-a交y轴于点B,记过点A且与直线l1相切的圆的圆心为点C.
已知定点A(0,a)(a>0),直线l1:y=-a交y轴于点B,记过点A且与直线l1相切的圆的圆心为点C. 某海海岸线可以近似的看成直线,位于岸边A处 的海警发现海中B处有人求救,该海警没有直接从A处游向B处,而是沿岸边自A跑到距离B最近的D处,然后游向B处,若海警在岸边的行进速度是6米/秒,在海中的行进速度是2米/秒,(不考虑水流速度等因素)
某海海岸线可以近似的看成直线,位于岸边A处 的海警发现海中B处有人求救,该海警没有直接从A处游向B处,而是沿岸边自A跑到距离B最近的D处,然后游向B处,若海警在岸边的行进速度是6米/秒,在海中的行进速度是2米/秒,(不考虑水流速度等因素) 已知F1、F2为为双曲线C:
已知F1、F2为为双曲线C: