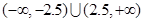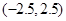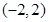题目内容
函数 是偶函数,它在
是偶函数,它在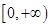 上是减函数.若
上是减函数.若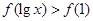 ,则
,则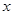 的取值范围是
的取值范围是
A.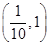 | B.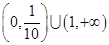 |
C.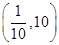 | D.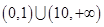 |
C
解析试题分析:根据偶函数的性质将f(lgx)>f(1)转化成f(|lgx|)>f(1),然后利用单调性建立不等关系,解之即可.
:∵f(x)定义在实数集R上的偶函数,
∴f(-x)=f(x)=f(|x|)则f(lgx)>f(1),即f(|lgx|)>f(1),
∵在区间[0,+∞)上是单调增函数
∴|lgx|<1即1>lgx>-1
∴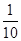 <x<10,故答案为:(
<x<10,故答案为:(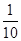 ,10),选C.
,10),选C.
考点:本题主要是考查函数奇偶性的应用,属于中档题
点评:解题的关键是由偶函数的性质,将f(lgx)≤f(1)转化成f(|lgx|)≤f(1),,同时利用单调性得到不等式组求解。

练习册系列答案
 金钥匙试卷系列答案
金钥匙试卷系列答案
相关题目
已知函数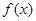 的定义域为
的定义域为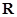 ,满足
,满足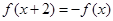 ,当
,当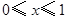 时,
时,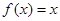 ,则
,则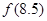 等( )
等( )
A.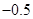 | B.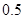 | C.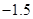 | D.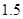 |
若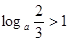 ,则a的取值范围是( )
,则a的取值范围是( )
A.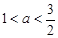 | B.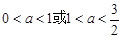 |
C.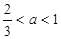 | D.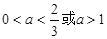 |
函数 的单调递减区间是 ( )
的单调递减区间是 ( )
A. | B. | C. | D. |
函数y= 的值域是[-2,2],则函数y=
的值域是[-2,2],则函数y=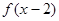 的值域是( )
的值域是( )
| A.[-2,2] | B.[-4,0] | C.[0,4] | D.[-1,1] |
函数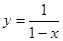 的图像与函数
的图像与函数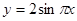 (
(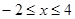 )的图像所有交点的横坐标之和等于 ( )
)的图像所有交点的横坐标之和等于 ( )
| A.2 | B.4 | C.6 | D.8 |
若R上的奇函数 的图象关于直线
的图象关于直线 对称,且当
对称,且当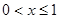 时,
时, ,则方程
,则方程 在区间
在区间 内的所有实数根之和为( )
内的所有实数根之和为( )
| A.4020 | B.4022 | C.4024 | D.4026 |
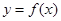 的图象为折线
的图象为折线 ,设
,设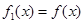 ,
,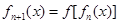 ,
,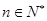 ,则函数
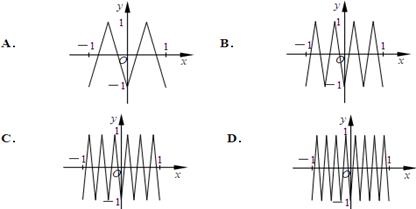
,则函数 的图象为( )
的图象为( ) 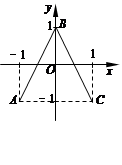
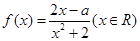 在区间
在区间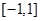 上是增函数,实数a组成几何A,设关于x的方程
上是增函数,实数a组成几何A,设关于x的方程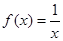 的两个非零实根
的两个非零实根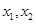 ,实数m使得不等式
,实数m使得不等式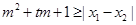 使得对任意
使得对任意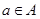 及
及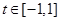 恒成立,则m的解集是( )
恒成立,则m的解集是( )