题目内容
函数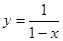 的图像与函数
的图像与函数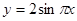 (
(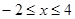 )的图像所有交点的横坐标之和等于 ( )
)的图像所有交点的横坐标之和等于 ( )
| A.2 | B.4 | C.6 | D.8 |
D
解析试题分析:函数y1=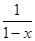 ,y2=2sinπx的图象有公共的对称中心(1,0),作出两个函数的图象如图
,y2=2sinπx的图象有公共的对称中心(1,0),作出两个函数的图象如图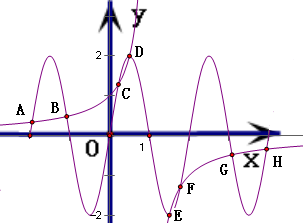
当1<x≤4时,y1<0
而函数y2在(1,4)上出现1.5个周期的图象,
在(1,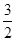 )和(
)和(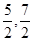 )上是减函数;
)上是减函数;
在(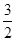 ,
,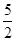 )和(
)和(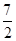 ,4)上是增函数.
,4)上是增函数.
∴函数y2在(1,4)上函数值为负数,且与y1的图象有四个交点E、F、G、H
相应地,y2在(-2,1)上函数值为正数,且与y1的图象有四个交点A、B、C、D
且:xA+xH=xB+xG═xC+xF=xD+xE=2,故所求的横坐标之和为8
故选D
考点:本题主要是考查图像与图像的交点问题的运用,体现了数形结合思想的运用。
点评:发现两个图象公共的对称中心是解决本题的入口,讨论函数y2=2sinπx的单调性找出区间(1,4)上的交点个数是本题的难点所在,。

练习册系列答案
相关题目
已知函数
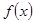 是定义在
是定义在 上的偶函数,当
上的偶函数,当 时,
时, ,那么函数
,那么函数
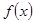 的零点个数为( )
的零点个数为( )
| A.一定是2 | B.一定是3 | C.可能是2也可能是3 | D.可能是0 |
函数 是偶函数,它在
是偶函数,它在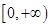 上是减函数.若
上是减函数.若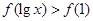 ,则
,则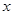 的取值范围是
的取值范围是
A.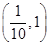 | B.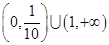 |
C.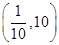 | D.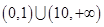 |
函数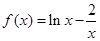 的零点所在的大致区间是( )
的零点所在的大致区间是( )
A.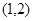 | B.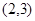 | C.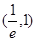 | D.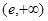 |
具有性质: 的函数,我们称为满足“倒负”变换的函数,下列函数:①
的函数,我们称为满足“倒负”变换的函数,下列函数:① ;②
;② ;③
;③ 中满足“倒负”变换的函数是( )
中满足“倒负”变换的函数是( )
| A.①② | B.①③ | C.②③ | D.只有① |
已知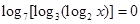 ,那么
,那么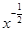 等于( )
等于( )
A.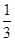 | B.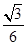 | C.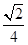 | D.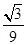 |
函数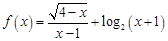 的定义域为( )
的定义域为( )
A.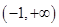 | B.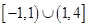 | C.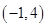 | D.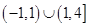 |
设函数
 的图象关于直线
的图象关于直线 及直线
及直线 对称,且
对称,且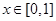 时,
时, ,则
,则 ( )
( )
A. | B. | C. | D. |
 满足
满足 ,且x∈[-1,1]时,
,且x∈[-1,1]时,  则函数h(x)=f(x)一g(x)在区间[-5,5]内的与x轴交点的个数为
则函数h(x)=f(x)一g(x)在区间[-5,5]内的与x轴交点的个数为