题目内容
(本小题满分14分)在数列 。
。
(1)求证:数列 是等差数列,并求数列
是等差数列,并求数列 的通项公式
的通项公式 ;
;
(2)设 ,求数列
,求数列 的前
的前 项和。
项和。
(1)  ;(2)
;(2)  .
.
【解析】
试题分析:(1)利用等差数列的定义 常数进行证明,进而求出
常数进行证明,进而求出 ,在利用
,在利用 与
与 的关系求出
的关系求出 ;(2)利用错位相减法进行求和.
;(2)利用错位相减法进行求和.
解题思路:1.证明等差数列的基本方法有:定义法与中项法;2.对于数列 (其中
(其中 是等差数列,
是等差数列, 是等比数列)的求和问题,采用错位相减法进行求和.
是等比数列)的求和问题,采用错位相减法进行求和.
试题解析:(1)证明:∵

 数列
数列 是等差数列 3分
是等差数列 3分
∵

由
 7分
7分
(2)由(1)的结论得 8分
8分
 ① 9分
① 9分
 ,② 10分
,② 10分
①-②,得
 13分
13分
 14分.
14分.
考点:1.等差数列;2.错位相减法.

练习册系列答案
相关题目
 ,命题
,命题 ,则命题
,则命题 是命题
是命题 成立的 ( )
成立的 ( ) (
(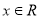 ,
,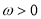 )的最小正周期为
)的最小正周期为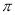 ,将
,将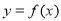 图像向左平移
图像向左平移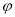 个单位长度
个单位长度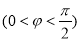 所得图像关于
所得图像关于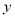 轴对称,则
轴对称,则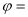 .
. 的值域为 .
的值域为 . 的图像不过第二象限时,
的图像不过第二象限时, 的取值范围是( )
的取值范围是( ) B.
B. C.
C. D.
D.
 ,b=3a,求△ABC的面积.
,b=3a,求△ABC的面积.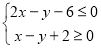 ,若目标函数z=ax+by(a>0,b>0)的最大值为40,则
,若目标函数z=ax+by(a>0,b>0)的最大值为40,则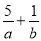 的最小值为( )
的最小值为( ) 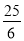 B、
B、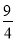 C、1 D、4
C、1 D、4 的解集是 .
的解集是 .