题目内容
8.在△ABC中,a,b,c分别为角A,B,C的对边,且$\frac{c}{b}$=-3cosA,tanB=$\frac{1}{2}$.(1)求tanA;
(2)若b=$\sqrt{5}$,求sinC.
分析 (1)利用正弦定理结合两角和差的正切公式进行化简即可求tanA;
(2)求出tanC,可得sinC.
解答 解:(1)在△ABC中,∵$\frac{c}{b}$=-3cosA,
∴sinC=-3sinBcosA,
∴sin(B+A)=-3sinBcosA,
∴sinBcosA+cosBsinA=-3sinBcosA,
∴cosBsinA=-4sinBcosA,
∴tanA=-4tanB,
∵tanB=$\frac{1}{2}$,∴tanA=-2;
(2)tanC=-tan(A+B)=-$\frac{-2+\frac{1}{2}}{1-(-2)•\frac{1}{2}}$=-$\frac{3}{4}$,
∴sinC=$\frac{3}{5}$.
点评 本题主要考查三角函数值的计算,利用正弦定理以及两角和差的正切公式是解决本题的关键.

练习册系列答案
 千里马走向假期期末仿真试卷寒假系列答案
千里马走向假期期末仿真试卷寒假系列答案
相关题目
19.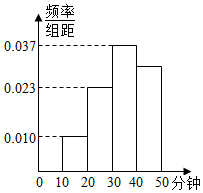 学校为了解学生每月购买学习用品方面的支出情况,抽取了n名学生进行调查,结果显示这些学生的支出(单位:元)都在[10,50]内,其频率分布直方图如图所示,其中支出在[10,30)内的学生有66人,则支出在[40,50]内的学生人数是( )
学校为了解学生每月购买学习用品方面的支出情况,抽取了n名学生进行调查,结果显示这些学生的支出(单位:元)都在[10,50]内,其频率分布直方图如图所示,其中支出在[10,30)内的学生有66人,则支出在[40,50]内的学生人数是( )
 学校为了解学生每月购买学习用品方面的支出情况,抽取了n名学生进行调查,结果显示这些学生的支出(单位:元)都在[10,50]内,其频率分布直方图如图所示,其中支出在[10,30)内的学生有66人,则支出在[40,50]内的学生人数是( )
学校为了解学生每月购买学习用品方面的支出情况,抽取了n名学生进行调查,结果显示这些学生的支出(单位:元)都在[10,50]内,其频率分布直方图如图所示,其中支出在[10,30)内的学生有66人,则支出在[40,50]内的学生人数是( )| A. | 30 | B. | 40 | C. | 60 | D. | 120 |
13.已知函数f(x)=sinx,g(x)=$\sqrt{3}$cosx,直线x=m与f(x),g(x)的图象分别交于M,N两点,则|MN|的最大值为( )
| A. | 2 | B. | $\sqrt{2}$ | C. | 2$\sqrt{2}$ | D. | 4 |
 如图,在实施棚户区改造工程中,某居委会决定对AF地段上的危旧房进行推平改建,拟在EF地段上新建一幢居民安置楼,在EF安置楼正南面的AB地段上建一个活动中心,活动中心的侧面图由两部分构成,下部分ABCD是矩形,上部分是以CD为直径的半圆O,活动中心的规划设计需满足以下要求:①AE=30米;②AB≥AD;③当地“最斜光线”与水平线的夹角α满足tanα=$\frac{3}{4}$,活动中心在当地“最斜光线”照射下落在EF安置楼上的影长GE不超过$\frac{5}{2}$米.
如图,在实施棚户区改造工程中,某居委会决定对AF地段上的危旧房进行推平改建,拟在EF地段上新建一幢居民安置楼,在EF安置楼正南面的AB地段上建一个活动中心,活动中心的侧面图由两部分构成,下部分ABCD是矩形,上部分是以CD为直径的半圆O,活动中心的规划设计需满足以下要求:①AE=30米;②AB≥AD;③当地“最斜光线”与水平线的夹角α满足tanα=$\frac{3}{4}$,活动中心在当地“最斜光线”照射下落在EF安置楼上的影长GE不超过$\frac{5}{2}$米.