题目内容
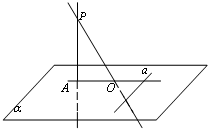
设平面α∥平面β,A,C∈α,B,D∈β,直线AB与CD交于点S,且点S位于平面α,β之间,AS=8,BS=6,CS=12,则SD=______.
根据题意做出如下图形:
∵AB,CD交于S点
∴三点确定一平面,所以设ASC平面为n,于是有n交α于AC,交β于DB,
∵α,β平行
∴AC∥DB
∴△ASC∽△DSB
∴
=
∵AS=8,BS=6,CS=12
∴
=
∴SD=9.
故答案为:9.

∵AB,CD交于S点
∴三点确定一平面,所以设ASC平面为n,于是有n交α于AC,交β于DB,
∵α,β平行
∴AC∥DB
∴△ASC∽△DSB
∴
| AS |
| SB |
| CS |
| SD |
∵AS=8,BS=6,CS=12
∴
| 8 |
| 6 |
| 12 |
| SD |
∴SD=9.
故答案为:9.


练习册系列答案
相关题目