题目内容
(本题满分12分)
若 ,且
,且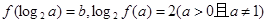 ,
,
(1)求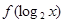 的最小值及相应 x的值;
的最小值及相应 x的值;
(2)若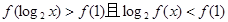 ,求x的取值范围.
,求x的取值范围.
(1)f (log2x)有最小值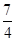 ,x=
,x=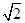 (2)0<x<1
(2)0<x<1
解析试题分析:(1)∵f (x)=x2-x+b,∴f (log2a)= (log2a)2-log2a+b=b,∴log2a=1∴a=2. ……2分
又∵log2f(a)=2,f(a)=4.∴a2-a+b=4,∴b=2.∴f (x)=x2-x+2 ……4分
∴f (log2x)= (log2x)2-log2x+2= (log2x- )2+
)2+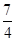 ,
,
∴当log2x= ,即x=
,即x=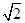 时,f (log2x)有最小值
时,f (log2x)有最小值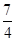 . ……6分
. ……6分
(2)由题意知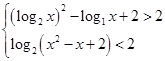 ……8分
……8分
∴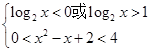 ……10分
……10分
∴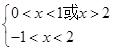 ∴ 0<x<1 ……12分
∴ 0<x<1 ……12分
考点:函数求解析式及解不等式
点评:求函数解析式主要用到的是待定系数法,整道题目在求解过程中多处涉及到了对数运算需结合对数函数性质考虑,整体来看难度不大,需分析求解时认真细心

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
 .
.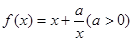 .
. 在定义域上的单调性;
在定义域上的单调性;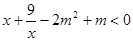 在
在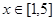 上恒成立时的实数
上恒成立时的实数 的取值范围?
的取值范围?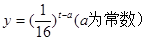 ,如图所示。
,如图所示。
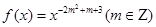 为偶函数,且在
为偶函数,且在 上为增函数.
上为增函数. 的值,并确定
的值,并确定 的解析式;
的解析式; 且
且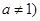 ,是否存在实数
,是否存在实数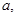 使
使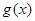 在区间
在区间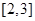 上的最大值为2,若存在,求出
上的最大值为2,若存在,求出 的值,若不存在,请说明理由.
的值,若不存在,请说明理由.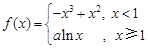 ,其中
,其中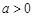
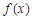 在
在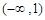 上的单调区间;
上的单调区间;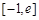 (
(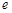 为自然对数的底数)上的最大值;
为自然对数的底数)上的最大值;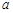 ,曲线
,曲线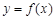 上是否存在两点
上是否存在两点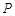 、
、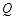 ,使得
,使得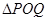 是以原点
是以原点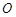 为直角顶点的直角三角形,且此三角形斜边中点在
为直角顶点的直角三角形,且此三角形斜边中点在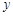 轴上?
轴上? (元)与月处理量
(元)与月处理量 (吨)之间的函数关系可近似的表示为:
(吨)之间的函数关系可近似的表示为: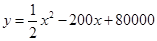 ,且每处理一吨二氧化碳得到可利用的化工产品价值为100元.
,且每处理一吨二氧化碳得到可利用的化工产品价值为100元. 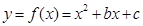 的图象过点(1,13),图像关于直线
的图象过点(1,13),图像关于直线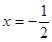 对称。
对称。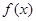 的解析式。
的解析式。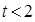 ,
,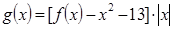 ,
,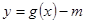 的零点有三个,求实数
的零点有三个,求实数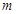 的取值范围;
的取值范围;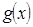 在[
在[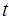 ,2]上的最小值。
,2]上的最小值。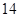 分)
分) 在定义域
在定义域 内某区间
内某区间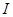 上是增函数,而
上是增函数,而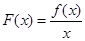 在
在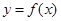 在
在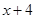 ,
,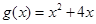 在
在 是否是“弱增函数”,
是否是“弱增函数”,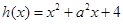 (
( 是常数且
是常数且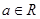 )在
)在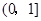 上是“弱增函数”.
上是“弱增函数”.