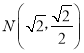Question

【题目】设F是椭圆的左焦点，过点F且斜率为正的直线与E相交于A、B两点，过点A、B分别作直线AM和BN满足AM⊥l，BN⊥l，且直线AM、BN分别与x轴相交于M和N.试求|MN|的最小值.

Answer 1

【答案】

【解析】

设，根据余弦定理，求得，再建立倾斜角和的函数关系，再利用三元不等式即可求得的最小值.

设过椭圆E左焦点F的直线l的倾斜角为，依题意知.

如图所示，设F'为椭圆E的右焦点，Rt△MAF中，cos∠MFA=，

所以有.

在Rt△NBF中，同理有，所以有：

. ①

连结BF'，在△FBF'中，记|BF|=x，则|BF'|=.

由余弦定理知，

即.

所以有，即. ②

同理有 ③

由②③知.

由①知.

令，则.

根据均值不等式知.

所以，

等号成立当且仅当，即.

所以当且仅当时，.

从而当且仅当时，.