题目内容
 如图所示,已知圆C:(x+1)2+y2=8,定点A(1,0),M为圆上一动点,点P在AM上,点N在CM上,且满足AM=2AP,NP⊥AM,点N的轨迹为曲线E.
如图所示,已知圆C:(x+1)2+y2=8,定点A(1,0),M为圆上一动点,点P在AM上,点N在CM上,且满足AM=2AP,NP⊥AM,点N的轨迹为曲线E.
(1)求曲线E的方程;
(2)若过定点F(0,2)的直线l交曲线E于不同的两点G、H(点G在点F、H之间),且满足 ,求直线l的方程;
,求直线l的方程;
(3)设曲线E的左右焦点为F1,F2,过F1的直线交曲线于Q,S两点,过F2的直线交曲线于R,T两点,且QS⊥RT,垂足为W;
(ⅰ)设W(x0,y0),证明: ;
;
(ⅱ)求四边形QRST的面积的最小值.
解:(1)∵NP为AM的中垂线
∴NA=NM
∴NA+NC=CM=2
∴N的轨迹为A,C为焦点的椭圆2a=2
∴ ,c=1
,c=1
∴b=1
∴方程为
(2)当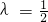 时,即G为FH中点时,设G(x1,y1)、H(x2,y2)
时,即G为FH中点时,设G(x1,y1)、H(x2,y2)
∴ ,代入椭圆得
,代入椭圆得 ,
,
∴
∴
∴
(3)(i)∵由过F1的直线交曲线于Q,S两点,过F2的直线交曲线于R,T两点,且QS⊥RT
∴W在以F1F2为直径的圆上,F1F2=2
∴x02+y02=1
∴
(ii)设QS的方程为y=k(x+1)(当k存在且不为0时)
代入
∴(1+2k2)x2+4k2x+2k2-2=0
设Q(x3,y3),S(x4,y4)
∴ ,
,
∴ ,
,
∵QS⊥RT
∴ ,同理,
,同理,
∴ ≥
≥ (当且仅当k2=1时,取等号)
(当且仅当k2=1时,取等号)
当k不存在或k=0时,
∵
∴
分析:(1)由于AM=2AP且NP⊥AM即NP为AM的中垂线故联想到连接NA即可观察出NA+NC=CM=2 在根据圆锥曲线的定义可写出曲线E的方程.
在根据圆锥曲线的定义可写出曲线E的方程.
(2)设G(x1,y1)、H(x2,y2)根据 可利用定比分点坐标公式(
可利用定比分点坐标公式(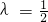 )找到点G,H的坐标间的关系然后代入到曲线E的方程可求出点D或G再根据直线的斜率公式求出斜率后有点斜式直接写出直线方程.
)找到点G,H的坐标间的关系然后代入到曲线E的方程可求出点D或G再根据直线的斜率公式求出斜率后有点斜式直接写出直线方程.
(3)(i)由过F1的直线交曲线于Q,S两点,过F2的直线交曲线于R,T两点,且QS⊥RT可得出W在以F1F2为直径的圆上且F1F2=2,F1(-1,0),F2(1,0)可得出w满足x02+y02=1再利用 进行放缩即可得证.
进行放缩即可得证.
(ii)当斜率不存在或斜率为0时易得面积S= ,当斜率存在时设为k则可得QS的方程为y=k(x+1)同时设Q(x3,y3),S(x4,y4)可令y=k(x+1)与
,当斜率存在时设为k则可得QS的方程为y=k(x+1)同时设Q(x3,y3),S(x4,y4)可令y=k(x+1)与 联立可求出x3+x4,x3x4后可利用弦长公式求出|QS|,再用-
联立可求出x3+x4,x3x4后可利用弦长公式求出|QS|,再用- 代替|QS|中的k即得到|RT|即可得出四边形QRST的面积的表达式然后利用均值不等求出最小值,再将此最小值与
代替|QS|中的k即得到|RT|即可得出四边形QRST的面积的表达式然后利用均值不等求出最小值,再将此最小值与 比较大小即可求出面积的最小值.
比较大小即可求出面积的最小值.
点评:本题是直线与圆锥曲线的综合问题的考查,是综合题有一定的难度.主要考查了利用圆锥曲线的定义求曲线方程(第一问),利用定比分点公式结合曲线方程求直线方程(第二问),利用圆的定义证明不等式和利用直线和曲线连立以及弦长公式求面积的最小值(第三问).同时题目中还涉及到了斜率存在与不存在的讨论,这也是分类讨论思想在解题中的应用的一个体现!
∴NA=NM
∴NA+NC=CM=2

∴N的轨迹为A,C为焦点的椭圆2a=2

∴
 ,c=1
,c=1∴b=1
∴方程为

(2)当
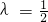 时,即G为FH中点时,设G(x1,y1)、H(x2,y2)
时,即G为FH中点时,设G(x1,y1)、H(x2,y2)∴
 ,代入椭圆得
,代入椭圆得 ,
,∴

∴

∴

(3)(i)∵由过F1的直线交曲线于Q,S两点,过F2的直线交曲线于R,T两点,且QS⊥RT
∴W在以F1F2为直径的圆上,F1F2=2
∴x02+y02=1
∴

(ii)设QS的方程为y=k(x+1)(当k存在且不为0时)
代入

∴(1+2k2)x2+4k2x+2k2-2=0
设Q(x3,y3),S(x4,y4)
∴
 ,
,∴
 ,
,∵QS⊥RT
∴
 ,同理,
,同理,
∴
 ≥
≥ (当且仅当k2=1时,取等号)
(当且仅当k2=1时,取等号)当k不存在或k=0时,

∵

∴

分析:(1)由于AM=2AP且NP⊥AM即NP为AM的中垂线故联想到连接NA即可观察出NA+NC=CM=2
 在根据圆锥曲线的定义可写出曲线E的方程.
在根据圆锥曲线的定义可写出曲线E的方程.(2)设G(x1,y1)、H(x2,y2)根据
 可利用定比分点坐标公式(
可利用定比分点坐标公式(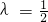 )找到点G,H的坐标间的关系然后代入到曲线E的方程可求出点D或G再根据直线的斜率公式求出斜率后有点斜式直接写出直线方程.
)找到点G,H的坐标间的关系然后代入到曲线E的方程可求出点D或G再根据直线的斜率公式求出斜率后有点斜式直接写出直线方程.(3)(i)由过F1的直线交曲线于Q,S两点,过F2的直线交曲线于R,T两点,且QS⊥RT可得出W在以F1F2为直径的圆上且F1F2=2,F1(-1,0),F2(1,0)可得出w满足x02+y02=1再利用
 进行放缩即可得证.
进行放缩即可得证.(ii)当斜率不存在或斜率为0时易得面积S=
 ,当斜率存在时设为k则可得QS的方程为y=k(x+1)同时设Q(x3,y3),S(x4,y4)可令y=k(x+1)与
,当斜率存在时设为k则可得QS的方程为y=k(x+1)同时设Q(x3,y3),S(x4,y4)可令y=k(x+1)与 联立可求出x3+x4,x3x4后可利用弦长公式求出|QS|,再用-
联立可求出x3+x4,x3x4后可利用弦长公式求出|QS|,再用- 代替|QS|中的k即得到|RT|即可得出四边形QRST的面积的表达式然后利用均值不等求出最小值,再将此最小值与
代替|QS|中的k即得到|RT|即可得出四边形QRST的面积的表达式然后利用均值不等求出最小值,再将此最小值与 比较大小即可求出面积的最小值.
比较大小即可求出面积的最小值.点评:本题是直线与圆锥曲线的综合问题的考查,是综合题有一定的难度.主要考查了利用圆锥曲线的定义求曲线方程(第一问),利用定比分点公式结合曲线方程求直线方程(第二问),利用圆的定义证明不等式和利用直线和曲线连立以及弦长公式求面积的最小值(第三问).同时题目中还涉及到了斜率存在与不存在的讨论,这也是分类讨论思想在解题中的应用的一个体现!

练习册系列答案
相关题目
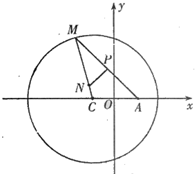 如图所示,已知圆C:(x+1)2+y2=8,定点A(1,0),M为圆上一动点,点P在AM上,点N在CM上,且满足
如图所示,已知圆C:(x+1)2+y2=8,定点A(1,0),M为圆上一动点,点P在AM上,点N在CM上,且满足| AM |
| AP |
| NP |
| AM |
A、
| ||
B、
| ||
C、x2+
| ||
D、x2-
|
 如图所示,已知圆C:(x+1)2+y2=8,定点A(1,0),M为圆C上一动点,点P在线段AM上,点N在线段CM上,且满足
如图所示,已知圆C:(x+1)2+y2=8,定点A(1,0),M为圆C上一动点,点P在线段AM上,点N在线段CM上,且满足 (理)如图所示,已知圆C:(x+1)2+y2=8,定点A(1,0),M为圆上一动点,点P在AM上,点N在CM上,且满足
(理)如图所示,已知圆C:(x+1)2+y2=8,定点A(1,0),M为圆上一动点,点P在AM上,点N在CM上,且满足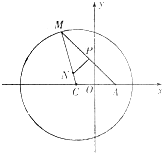 如图所示,已知圆C:(x+1)2+y2=8,定点A(1,0),M为圆上一动点,点P在AM上,点N在CM上,且满足AM=2AP,NP⊥AM,点N的轨迹为曲线E.
如图所示,已知圆C:(x+1)2+y2=8,定点A(1,0),M为圆上一动点,点P在AM上,点N在CM上,且满足AM=2AP,NP⊥AM,点N的轨迹为曲线E. (2006•石景山区一模)如图所示,已知圆C:(x+1)2+y2=8,定点A(1,0),M为圆上一动点,点P在AM上,点N在CM上,且满足
(2006•石景山区一模)如图所示,已知圆C:(x+1)2+y2=8,定点A(1,0),M为圆上一动点,点P在AM上,点N在CM上,且满足