题目内容
1．两个平面可以把空间分成3或4部分，三个平面可以把空间分成4或6或7或8部分．分析 由已知条件利用平面平行或相交的位置关系分类讨论，能求出结果．
解答 解：当两个平面平行时，可以把空间分为3个部分，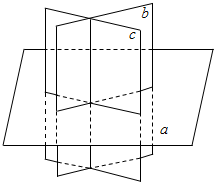
当两个平面相交时，可以把空间分为4个部分，
当三个平面平行时，可以把空间分为4个部分，
当三个平面中两个平行，另一个分别和两个平行平面相交，可以把空间分为6个部分，
当三个平面两两相交时，可以把空间分为6或7或8部分，
当两个面相交成十字，第三个面与两个面的交线垂直，可以把空间分成8个部分，如右图，
∴两个平面可以把空间分成3或4部分；
三个平面可以把空间分成4或6或7或8部分．
故答案为：3或4，4或6或7或8．
点评 本题考查平面把空间分成几部分的判断，是中档题，解题时要注意分类讨论思想的合理运用．
练习册系列答案
灵星计算小达人系列答案
相关题目
9．
如图，在棱长为3的正方体ABCD-A1B1C1D1中，M为线段B1C1上的动点，则三棱锥M-BCD1的体积为（ ）（参考结论：若一条直线与一个平面平行，则该直线上的动点到此平面的距离是一个定值）
如图，在棱长为3的正方体ABCD-A1B1C1D1中，M为线段B1C1上的动点，则三棱锥M-BCD1的体积为（ ）（参考结论：若一条直线与一个平面平行，则该直线上的动点到此平面的距离是一个定值）| A． | 3 | B． | $\frac{9}{2}$ | C． | 9 | D． | 与M点的位置有关 |
16．棱长为a的正方体ABCD-A1B1C1D1中，与D1B平行的平面截正方体所得截面面积为S，则S的取值范围是（ ）
| A． | （ 0，$\frac{\sqrt{6}{a}^{2}}{2}$） | B． | （0，$\frac{3\sqrt{3}{a}^{2}}{4}$] | C． | （0，$\frac{5{a}^{2}}{4}$） | D． | （0，$\frac{\sqrt{6}{a}^{2}}{4}$] |
13．已知函数f（x）=|cosx|•sinx，给出下列四个说法，其中正确说法是（ ）
| A． | 若|f（x1）|=|f（x2）|，则x1=x2+kπ（k∈Z） | B． | f（x）在区间$[-\frac{π}{4}，\frac{π}{4}]$上单调递增 | ||
| C． | 函数f（x）的周期为π | D． | f（x）的图象关于点$（-\frac{π}{2}，0）$成中心对称 |
11．已知集合A={x|x2-x-6＜0}，$B=\{x\left|{y=\sqrt{x-m}}\right.\}$．若A∩B≠∅，则实数m的取值范围是（ ）
| A． | （-∞，3） | B． | （-2，3） | C． | （-∞，-2） | D． | [3，+∞） |