题目内容
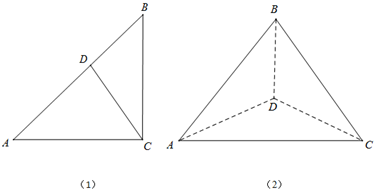
8.如果PA、PB、PC两两垂直,那么点P在平面ABC内的投影一定是△ABC( )| A. | 重心 | B. | 内心 | C. | 外心 | D. | 垂心 |
分析 根据题意画出图形,如图P是△ABC所在平面外一点,O是P点在平面ABC上的射影.然后利用线面的位置关系进行判定即可.
解答 解:若PA、PB、PC两两互相垂直,
可得AP⊥平面PBC,BP⊥平面PAC,CP⊥平面PAB,
由此可证得BC⊥OA,AB⊥OC,AC⊥OB,
即此时点O是三角形三边高的交点,
故此时点O是三角形的垂心,
故选:D.
点评 本题考查棱锥的结构特征,考查学生发现问题解决问题的能力,是中档题.

练习册系列答案
相关题目
18.关于x的不等式x2-ax+a>0恒成立,则实数a的取值范围为( )
| A. | (-∞,0)∪(2,+∞) | B. | (0,2) | C. | (-∞,0)∪(4,+∞) | D. | (0,4) |
16.若不等式|x-2|+|x+3|<a的解集为∅,则a的取值范围为( )
| A. | (2,+∞) | B. | [-3,+∞) | C. | (-∞,5] | D. | (-∞,-3) |
3.一个球体经过切割后,剩下部分几何体的三视图如图所示,则剩下部分几何体的体积为( )
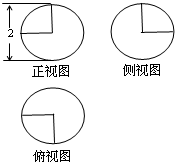

| A. | $\frac{7π}{6}$ | B. | $\frac{6π}{7}$ | C. | $\frac{4π}{3}$ | D. | $\frac{3π}{4}$ |
13.某电脑公司有6名产品推销员,其工作年限与年推销金额数据如表:
(1)求年推销金额y与工作年限x之间的相关系数(精确到0.01);
(2)求年推销金额y关于工作年限x的线性回归方程.
(参考数据:$\sqrt{1.04}$≈1.02.)
参考公式:线性相关系数公式:r=$\frac{\sum_{i=1}^{n}({x}_{i}-\overline{x})({y}_{i}-\overline{y})}{\sqrt{\sum_{i=1}^{n}({x}_{i}-\overline{x})^{2}\sum_{i=1}^{n}({y}_{i}-\overline{y})^{2}}}$
线性回归方程系数公式:$\hat y$=bx+a,其中b=$\frac{\sum_{i=1}^{n}({x}_{i}-\overline{x})({y}_{i}-\overline{y})}{\sum_{i=1}^{n}({x}_{i}-\overline{x})^{2}}$,a=$\overline{y}$-bx.
| 推销员编号 | 1 | 2 | 3 | 4 | 5 |
| 工作年限x/年 | 3 | 5 | 6 | 7 | 9 |
| 推销金额y/万元 | 2 | 3 | 3 | 4 | 5 |
(2)求年推销金额y关于工作年限x的线性回归方程.
(参考数据:$\sqrt{1.04}$≈1.02.)
参考公式:线性相关系数公式:r=$\frac{\sum_{i=1}^{n}({x}_{i}-\overline{x})({y}_{i}-\overline{y})}{\sqrt{\sum_{i=1}^{n}({x}_{i}-\overline{x})^{2}\sum_{i=1}^{n}({y}_{i}-\overline{y})^{2}}}$
线性回归方程系数公式:$\hat y$=bx+a,其中b=$\frac{\sum_{i=1}^{n}({x}_{i}-\overline{x})({y}_{i}-\overline{y})}{\sum_{i=1}^{n}({x}_{i}-\overline{x})^{2}}$,a=$\overline{y}$-bx.