题目内容
12.f(x)=x2+ax满足f(2-x)=f(2+x),则a=-2.分析 若f(a-x)=f(b+x),则f(c)的对称轴为x=$\frac{a+b}{2}$,即可求出答案.
解答 解:f(x)=x2+ax满足f(2-x)=f(2+x),
∴f(x)的对称轴为x=2,
∴-a=2,
即a=-2,
故答案为:-2
点评 本题考查了函数的对称轴的求法,属于基础题.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
20.已知数列{an}为等差数列,且a5+a7+a9+a11+a13=80,则a14+a16-a21=( )
| A. | 12 | B. | 15 | C. | 16 | D. | 18 |
4.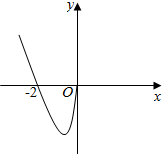 已知函数f(x)满足对任意x∈R都有f(x)+f(-x)=0,且在(-∞,0]上的图象如图所示,则关于x的不等式$\frac{f(x)-f(-x)}{x}$<0的解集为( )
已知函数f(x)满足对任意x∈R都有f(x)+f(-x)=0,且在(-∞,0]上的图象如图所示,则关于x的不等式$\frac{f(x)-f(-x)}{x}$<0的解集为( )
 已知函数f(x)满足对任意x∈R都有f(x)+f(-x)=0,且在(-∞,0]上的图象如图所示,则关于x的不等式$\frac{f(x)-f(-x)}{x}$<0的解集为( )
已知函数f(x)满足对任意x∈R都有f(x)+f(-x)=0,且在(-∞,0]上的图象如图所示,则关于x的不等式$\frac{f(x)-f(-x)}{x}$<0的解集为( )| A. | (-∞,-2)∪(2,+∞) | B. | (-2,0)∪(2,+∞) | C. | (-2,2) | D. | (-∞,-2)∪(0,2) |
11.已知命题p:对任意x∈R,总有|x|≥0;命题q:x=2是方程x+2=0的根.则下列命题为真命题的是( )
| A. | p∧¬q | B. | ¬p∧q | C. | ¬p∧¬q | D. | p∧q |